
I will put Chaos into fourteen lines--- Edna St. Vincent Millay
And keep him there; and let him thence escape
If he be lucky; let him twist, and ape
Flood, fire, and demon --- his adroit designs
Will strain to nothing in the strict confines
Of this sweet order, where, in pious rape,
I hold his essence and amorphous shape,
Till he with Order mingles and combines.
Past are the hours, the years of our duress,
His arrogance, our awful servitude:
I have him. He is nothing more nor less
Than something simple not yet understood;
I shall not even force him to confess;
Or answer. I will only make him good.
 Come watch the orbiting, leap-frogging zeroes of the
Riemann zeta function play out in the full glory of
the complex z-plane of the polylogarithm! Will any of them
ever miss? The Riemann Hypothesis says no! Huh?
Details here!
Come watch the orbiting, leap-frogging zeroes of the
Riemann zeta function play out in the full glory of
the complex z-plane of the polylogarithm! Will any of them
ever miss? The Riemann Hypothesis says no! Huh?
Details here!
 Other parts of this web site previously explored Arnold tongues.
This page revisits some of this old ground, but provides a different
perspective and emphasis, and explores maps that are simpler than the
circle map.
Other parts of this web site previously explored Arnold tongues.
This page revisits some of this old ground, but provides a different
perspective and emphasis, and explores maps that are simpler than the
circle map.
 Graphs of the analytic generating functions of the greatest prime factor
function. Very remarkably, there seems to be very little or nothing
known about these functions: they do not appear to have been studied
before! (Here is a PDF version of this page.)
Graphs of the analytic generating functions of the greatest prime factor
function. Very remarkably, there seems to be very little or nothing
known about these functions: they do not appear to have been studied
before! (Here is a PDF version of this page.)
 Graphs of the exponential generating functions of various popular
arithmetic functions from number theory. These are just ... awesome!
I promise, you've never seen anything like this before!
Graphs of the exponential generating functions of various popular
arithmetic functions from number theory. These are just ... awesome!
I promise, you've never seen anything like this before!
The Gap Theory Page reviews some of the mathematical underpinnings. The Gap Room explores images based on gaps. The F2 Room holds some additional, miscellaneous continued-fraction-based images.
 This room contains pictures of the Poincare Recurrence Time
of the damped circle-map.
This room contains pictures of the Poincare Recurrence Time
of the damped circle-map.
 Decorating the interior of a well know exterior -- an (increasingly fat) sketchbook of
ideas.
Decorating the interior of a well know exterior -- an (increasingly fat) sketchbook of
ideas.
 The Logistic Equation x[n+1] = lambda * x[n] * (1-x[n]) + omega
is in some ways a simplified version of the Circle Map
x[n+1] = lambda * sin (2*pi*x[n]) + x[n] + omega. In this room,
we explore further variations.
The Logistic Equation x[n+1] = lambda * x[n] * (1-x[n]) + omega
is in some ways a simplified version of the Circle Map
x[n+1] = lambda * sin (2*pi*x[n]) + x[n] + omega. In this room,
we explore further variations.
 More games with continued fraction mappings result in
constructed figures that bear a vague and superficial
resemblance to Poincare maps. This twisted mess is what
happens when you just say no to iteration.
More games with continued fraction mappings result in
constructed figures that bear a vague and superficial
resemblance to Poincare maps. This twisted mess is what
happens when you just say no to iteration.
 Images of famous number-theoretic functions. The goal is to provide
a visual overview of the SL(2,Z) modular group symmetry of these
functions. In development.
Images of famous number-theoretic functions. The goal is to provide
a visual overview of the SL(2,Z) modular group symmetry of these
functions. In development.
 Ahh ... the Post-Industrial Era. Err.. Futurist ... Ahh Dada ?
Well ... The usual Mandelbrot set, z(n+1) = z(n)*z(n) + c,
where c = r * exp (i*theta). Well, we've plotted theta along x-axis, and
r along y axis. A bit of a different view ... Hmmm?
Ahh ... the Post-Industrial Era. Err.. Futurist ... Ahh Dada ?
Well ... The usual Mandelbrot set, z(n+1) = z(n)*z(n) + c,
where c = r * exp (i*theta). Well, we've plotted theta along x-axis, and
r along y axis. A bit of a different view ... Hmmm?
 The artist's early period ........ wherein he experimented early with
periodicity ...............
The artist's early period ........ wherein he experimented early with
periodicity ...............
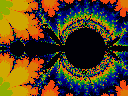 Circle Map Movies
Circle Map Movies
 A smooth, fractionally-valued, mathematically exact iteration count
can be defined for any iterated equation. This
Renormalized Iteration Count
removes the dependency of results on the number of
iterations and on the escape-radius. This theory is useful for
producing smooth, non-banded images.
A smooth, fractionally-valued, mathematically exact iteration count
can be defined for any iterated equation. This
Renormalized Iteration Count
removes the dependency of results on the number of
iterations and on the escape-radius. This theory is useful for
producing smooth, non-banded images.
Note that its closely related to the Douady-Hubbard potential whose field lines or external rays underpin the theoretical analysis of the M-set. Here's a brief Atlas of Rays, and an accompanying table of Arc Angles.
 The interior can be explored by taking derivatives. These derivatives have
interesting analytic behaviors.
The interior can be explored by taking derivatives. These derivatives have
interesting analytic behaviors.
 Penrose conjectures that the inside of the Mandelbrot set is
computationally undecidable, and Smale tries to prove the same.
We none-the-less provide an algorithm that seems to at least
come close.
Penrose conjectures that the inside of the Mandelbrot set is
computationally undecidable, and Smale tries to prove the same.
We none-the-less provide an algorithm that seems to at least
come close.
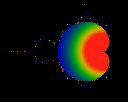 Interior points converge to limit cycles. A limit cycle that repeats
after N iterations can be averaged together to get an average value.
This page explores a technique for reliably computing smooth 'average
values' out of very unsmooth sequences. It appears that the interior
of the Mandelbrot Set is described by the Dedekind eta, providing yet
another tie between modular forms and fractals. A revised, updated
treatment of this topic can be found in the math
section.
Interior points converge to limit cycles. A limit cycle that repeats
after N iterations can be averaged together to get an average value.
This page explores a technique for reliably computing smooth 'average
values' out of very unsmooth sequences. It appears that the interior
of the Mandelbrot Set is described by the Dedekind eta, providing yet
another tie between modular forms and fractals. A revised, updated
treatment of this topic can be found in the math
section.
 An ongoing attempt to measure the size of, and characterize the shape of
the Mandelbrot set. We present a simple estimate of the bud sizes that is
good to about 5%; unfortunately, the buds aren't quite circular.
Includes supporting visual documentation.
An ongoing attempt to measure the size of, and characterize the shape of
the Mandelbrot set. We present a simple estimate of the bud sizes that is
good to about 5%; unfortunately, the buds aren't quite circular.
Includes supporting visual documentation.
 Ray-traced images of light passing through a simple cubic lattice
of reflective 'atoms' shows clearly the strongly ergodic nature
of Sinai's Billiards. An atlas of different sizes of balls and
lattices.
Ray-traced images of light passing through a simple cubic lattice
of reflective 'atoms' shows clearly the strongly ergodic nature
of Sinai's Billiards. An atlas of different sizes of balls and
lattices.

Yes, we have source code! (Warning -- its very ugly -- its way hacked.)
