Hacked Mandelbrot

Here is the usual Mandelbrot set, z(n+1) = z(n)*z(n) + c, where c = K * exp (i*theta). Well, we've plotted theta along x-axis, and K along y axis. K runs from 0.0 to 2.0, and theta from 0 to 2*pi. Why'd we do this? Because this is the parameterization resembles slightly that used in the circle map, and we want to explore the similarities.

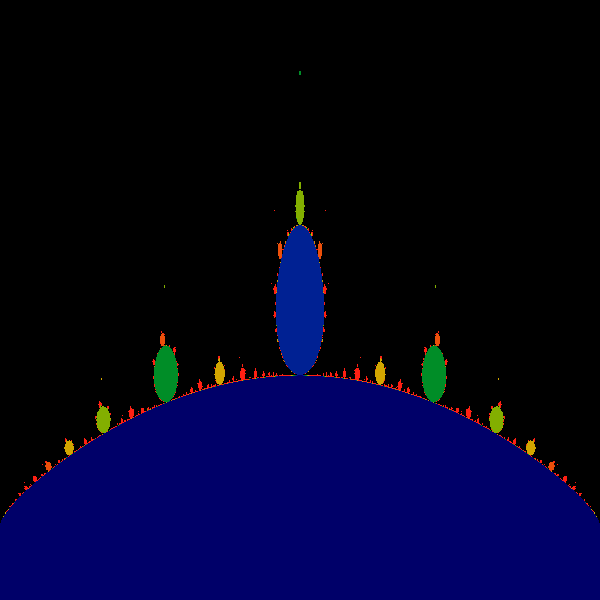
Well, the base looks pretty darn circular, right? Its not. It's ever so slightly eccentric (nothing in life is easy). The shape is given by the often quoted "cardiod", z = 0.5 * exp (i*phi) - 0.25 * exp (2*i*phi), which, in our coordinate system, K = 0.5 * sqrt (1.25 - cos(phi)) and theta = arctan ( (sin(phi) - 0.5*sin(2*phi)) / (cos(phi) - 0.5*cos(2*phi))). In this coordinate system, the cardiod is very nearly a circle, to within about 1% of the radius (graph), which I find to be a curious fact not to be forgotten when trying to find the shapes of things.

Another, perhaps more interesting mapping, not explored here, will flatten the cardiod to a line: Let

c = K e^it - K² e^2it

Thus we see the main cardiod lie below the straight line K=1/2. (and a reflected image above it at t=0, which is where the horn/butt maps to).

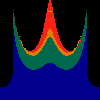
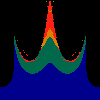
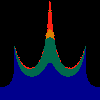
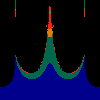
Now we start playing some distortion games. The images below represent the usual iteration, except that now, we start playing with the strength of the cross term. That is, instead of the usual

z <-- z*z + c  
   == (x+i*y)*(x+i*y)  + Re(c) + i*Im(c)
   == x*x - y*y + Re(c)  + i * (2*x*y + Im(c))

we play with the cross term ...

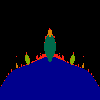
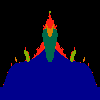
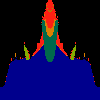
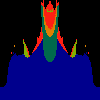
z <-- z*z + c  
   == (x+i*y)*(x+i*y)  + Re(c) + i*Im(c)
   == x*x - y*y + Re(c)  + i * (2*x*y(1.0-lambda) + Im(c))

In the sequence below, we see lambda go from 0.1 to 1.0, in steps of 0.1. Click on the prictures with the big borders.

In this next sequence, we have lambda from -0.1 to -1.5 in steps of 0.1

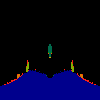
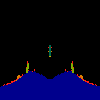
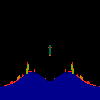
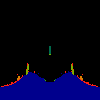
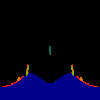
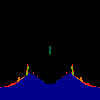
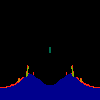
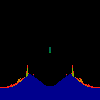
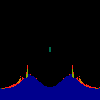
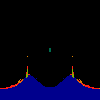
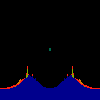
Hacked Mandelbrot by Linas Vepstas is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.