My hidden hope is, of course, that by the application of this theory, exact, analytic expressions can be presented for various fractal phenomena, such as the boundary of the Mandelbrot set, or the structure of phase locking in the circle map, without the use of iteration. Or, put in high-falutin terms, that homomorphisms between iterated functions and continued fractions can be found. I am not aware of any work (other than my own) that pertains to this goal, published on the web, or in traditional publications. Feel free to send me a pre-print, or re-print, or a URL, to me, at 1518 Enfield Road, Austin TX 78703-3424 USA, if you know better.
The exposition on this page is not deep: the presentation is straight-forward, and should be accessible to patient and smart high-school readers.
x = 1/(a1 + 1/(a2 + 1/(a3 + ... )))
Given any x, this sequence is straightforward to compute. Rational numbers x always have a finite number of terms in the sequence. For a rational number x, there are two distinct expansions that yield the same value:
x+ = [a1, a2, ... , aN]
and
x- = [a1, a2, ... , aN-1, 1]
In the following text, we make a simplifying notational confusion: we use the same symbols to denote a sequence and its value when expressed as a continued fraction. Thus, for the above sequences, we may write x = x- = x+. It will hopefully be obvious which is which.
Given a rational x and an arbitrary complex number w, define new sequences:
x+(w) = [a1, a2, ... , aN, 1/w]
x-(w) = [a1, a2, ... , aN-1, 1, 1/w]
These two functions are analytic in w, and can be expressed as the ratio of two polynomials in w. Thus, general analytic manipulations are perfectly well-defined on these functions. Clearly,
limw->0 x-(w) = limw->0 x+(w) = x
Differentiation w.r.t. w provides a handy tool for constructing various interesting things and proving various limits. We give an exact expression for these derivatives below. Although we've introduced w by appending it to the last term of a rational expansion, we could, if we wanted, introduce w into the N'th term of an irrational expansion. Most of the statements we make below are for rationals. This is in part because treating the irrationals is a bit harder and confusing, both in these formulas, and in their implementation as algorithms.
There is also an even-odd symmetry for x(w) that we should be aware of, as it plays another important role in the theory. As we point out above, for any given sequence, there is a + and a - generalization. But what if the sequence is already x- and we choose the - expansion? Then we get
x-- = [a1, a2, ... , aN-1, 0, 1]
This expansion invokes a symmetry on x-(w):
x--(w) = [a1, a2, ... , aN-1, 0, 1, 1/w] = x+(w)
Thus, we see that a double-expansion is either idempotent or alternating. To be pedantic, we can complete this with the other three expressions: x++(w) = x+(w) and x-+(w) = x+-(w) = x-(w). In other words, a double-expansion reflects back, and, in this sense, x+ and x- are unique. If one needs to take differences, e.g. for derivatives, the even-odd expansion is more useful: Define xe(w) and xo(w) as follows:
xe = [ if (N even) x+ else x- ]
xo = [ if (N even) x- else x+ ]
These have nice order-preserving properties: if w is a positive real, then
xo(w) < xe(w)
and, for negative real w,
xo(w) > xe(w)
and thus differences are well-behaved as a function of x.
These also have idempotent or parity-swapping identities:
xe+ = xe , xe- = xo , xo+ = xo , xo- = xe
xee = xe , xeo = xo , xoe = xe , xoo = xo
x+e = xe , x+o = xo , x-e = xe , x-o = xo
Fz(x) = z/(a1 + z/(a2 + z/(a3 + ... )))
For any rational x, Fz(x) is analytic in z. But, for any z not equal to one, it is continuous nowhere in x. Some beautiful pictures of this function and its cousins can be seen in the art gallery in the Farey Room. As can be seen from the pictures in the art-gallery, the discontinuities are reminiscent of various fractal phenomena. Our goal in this section is to characterize these discontinuities, or 'gaps'.
For rational x, just as we defined x-(w) and x+(w), it is handy to provide the same treatment for F, and thus define Fz(x+(w)) and Fz(x-(w)) in the obvious way. Note, in particular, that the +/- and even/odd symmetries still apply: in particular,
Fz([a1, a2, ... , aN-1, 0, 1, 1/w] ) = Fz([a1, a2, ... , aN-1, 1/w] )
It is in the analysis of Fz where the distinction between x+(w) and x-(w) becomes important: the discontinuitities can be precisely characterized as the difference between these. Let
D-z(x) = limw->0 [ Fz(xeven(w)) - Fz(xodd(w)) ]
This function is perfectly well-defined because it is the limit of a function that is analytic in w. It is still analytic in z, and is very discontinuous in x. (and we've side-stepped the issue of defining it for irrational x). D- essentially characterizes the discontinuities in F. Another interesting function is the symmetric sum: D+z(x) = limw->0 [ Fz(x+(w)) + Fz(x-(w)) ] = limw->0 [ Fz(xeven(w)) + Fz(xodd(w)) ]
Note that D-z goes to zero as z->1. We use this to define the 'gaps':
G-(x) = limz->1 D-z(x) / (z-1)
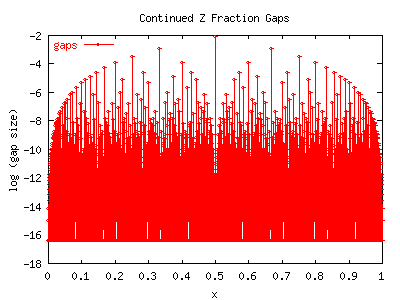
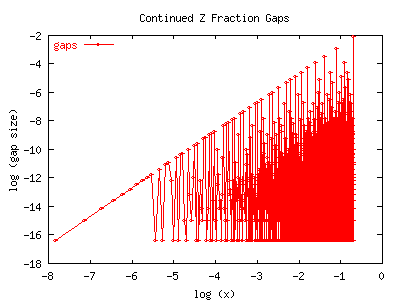
Again, because D was analytic in z, this limit is perfectly well defined for any rational x. Again, it is continuous nowhere in x. It is not terribly hard to compute numerically; it being well-defined leads to there being no numerical instabilities or inaccuracies that accumulate when computing it. It is very tractable with basic common-sense numerical programming techniques. The following two graphs show G-(x). If you look at them carefully, you can now spot the relationship to Farey numbers.


The tallest visual sequence corresponds to gaps at 1/2, 1/3, 1/4, ...,1/n. Where are the next-tallest gaps? If you squint carefully, you can see they are at the Farey mediants between their tallest neighbors. Thus, the second line is at 2/5, 2/7, 2/9, ... Similarly, the largest gap between 1/2 and 2/5 is at 3/7. The largest gap between 2/5 and 1/3 is at 3/8. By now, the sequence should be recognizable as a Farey Tree:
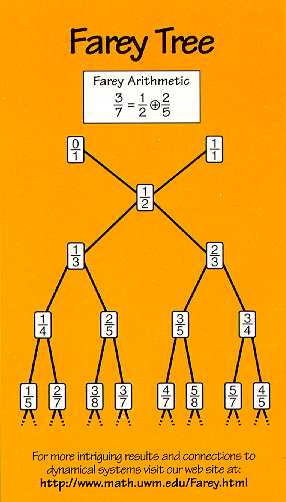
Theorem: The largest gaps are laid out on a Farey Tree.
Proof: Given any rational p/q, reduced so that p and q share no
common factors, we have G-(p/q) = 1/q2 (as shown below).
The largest gap is clearly at p/q=1/2. We can then apply the usual induction
on the Farey Tree: if p1/q1 and p2/q2
then
p1/q1 <
(p1+p2)/(q1+q2) =
p3/q3 < p2/q2
is true and
p2q1 = 1+p1q2 is also true.
Now we need to search for a fraction m/n with the smallest possible
denominator n that satisfies
p1/q1 < m/n < p2/q2.
Clearly, n =< q1+q2, we just proved that above.
To complete the proof, we need to show strict equality. Could n be smaller
than this? Well, suppose it's smaller by one. However,
(p1+p2-1) /
(q1+q2-1) =<
p1/q1
and
p2/q2 =<
(p1+p2) /
(q1+q2-1)
therefore
(q1+q2-1) != n and therefore
n can't be smaller by one. Is it smaller by two? Well, no, and if we work
out the recursion formula (its a bit tedious but maybe a good exercise),
we conclude n can't be smaller by two, three, or anything. Therefore
n = (q1+q2) is the smallest denominator, and thus,
the largest gap, that can occur between
p1/q1 and p2/q2.
By induction, the largest gaps are ordered on the Farey tree.
QED
I do not know if the above theorem is new, or is old and well known. I am not aware of any references, on the web, or published in journals, that deal with these 'gaps'. Please let me know if you have references. Note that the earliest theorems about Farey numbers were first proved by Haros in 1802, 14 years before Farey publicized the relationship that now bears his name. Maybe we should call them 'Haros Numbers'.
sk = ak + 1/sk+1
That is, we've defined sk such that x = 1/s1. It is handy to also define a0=0 so that we can write x = s0. The corresponding term in Fz(x) is tk with
tk = ak + z/tk+1
Because we will be taking the limits w->0 and z->1, we should expand tk to the first order in each. That is, assuming w and (z-1) are small, define
tk = sk + w Wk + (z-1)Dk + w(z-1)Ek
By applying the recurrence relation for tk we can deduce the recurrence relations for each of these pieces:
Dk-1 = (1 - Dk/sk)/sk
Wk-1 = - Wk/sk2
Ek-1 = - (Wk + Ek)/sk2
To these, we need to add the initial conditions. For F(x+) we have
sN = aN , DN = 0 , WN = 1 , EN = 1
and for F(x-) we have
sN = aN , DN = 1 , WN = -1 , EN = -2
It is handy to label each sequence with a + or - to denote the initial conditions. Thus, for example, to the first order in w and z-1,
Fz(x+(w)) = t+0 = s+0 + w W+0 + (z-1)D+0 + w(z-1)E+0
and so, for (z-1) << 1
D-z(x) = limw->0 (teven0 - todd0) = (z-1)(Deven0 - Dodd0)
and finally,
G-(x) = Deven0 - Dodd0
So computing G or any of the other functions is simply a matter of applying the recurrence relations.
The derivative of x w.r.t w is obtained in a similar manner:
dx(w)/dw |w=0 = ( dx+(w)/dw |w=0 + dx-(w)/dw |w=0) / 2 = ( W+0 + W-0) / 2
G+ (1/n) = 2/n - 1/n2
G- (1/n) = 1/n2.
G- (2/(2n+1)) = 1/(2n+1)2
G- (3/(3n+1)) = 1/(3n+1)2
G- (3/(3n+2)) = 1/(3n+2)2
G- (4/(4n+1)) = 1/(4n+1)2
G- (4/(4n+3)) = 1/(4n+3)2
G- (5/(5n+1)) = 1/(5n+1)2
G- (5/(5n+2)) = 1/(5n+2)2
G- (5/(5n+3)) = 1/(5n+3)2
G- (5/(5n+4)) = 1/(5n+4)2
G- (6/(6n+1)) = 1/(6n+1)2
G- (6/(6n+5)) = 1/(6n+5)2
And so on. I hope you see the obvious pattern for G-: Given any rational p/q, reduced so that p and q share no common factors, we have G-(p/q) = 1/q2
Copyright (c) 2000 Linas Vepstas
All Rights Reserved.
To contact Linas, see his
Home Page.