The Farey Room
The Farey Room shows the fractal relationships between Farey Fractions
through various transformations of continued fractions. These visualize
a fantastic set of continuous mappings of Cantor Sets and thier
fractal symmetries.
Click on the small icons to see larger, more detailed views.
Artistic Apologies, Dogmatic Disclaimers:
This material was originally presented (in the 1994 web page)
with graphic design sensibilities that were more
sparse, neutral, mystical and suggestive, which helped highlight
the intricately twisted patterns.
I now think (as of 2000) that more literate readers would rather enjoy a bit of
the actual mathematical background that goes into these pictures.
And so, I've added a small dose of math to the descriptions.
As there are now hundreds of web sites with far prettier
fractal artworks than my own, I am hoping that this tie between
theory and pixels proves refreshing and balanced.
My apologies
to the artistic types who would prefer darkness and mystery.
My apologies
to the mathematicians who see more beauty in theorems and proofs.
In search of grace, which must surely lie in between preferences.
Continued Fractions
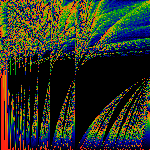
Palms
The above shows the most basic transformation, where all
occurrences of "1" in the numerator of continued fraction expansions
of the real number are replaced by "z".
That is, if x = 1/(a+1/(b+1/(c+1/(d+ ...))))
then fz(x) = 1/(a+z/(b+z/(c+z/(d+ ... )))).
We use fz(x) mod 1 to
generate a Hausdorff measure
for a given (x,z). The measure is shown as
a color, with black=zero, blue=small, green=larger, yellow=large, red=larger
still.
Along the horizontal axis, real numbers. Along the
vertical axis, z, ranging from +1 to -1 (+1 at bottom, -1 at top, 0 along
the midline).
Note the pseudo-Arnold's Tongues which occur for all irrational
values on the horizontal axis. This is essentially due to the fact that
the mapping is discontinuous for all rational values of x, and z != 1.
Note that a cross-section through this picture (a horizontal line
drawn through it) is a Cantor Set.
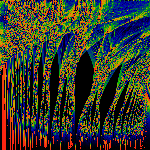
Waves
The unit modulus: |fz(x)| for z=eit. Along the vertical axis,
t=0 at the bottom, t=pi at the top.
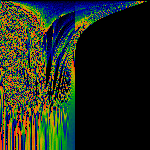
Seawall
The unit modulus: phase(fz(x))/t for z=eit. Along the vertical axis,
t=0 at the bottom, t=pi at the top.
One can play more complex games. If x =
1/(a1+1/(a2+1/(a3+1/(a4+ ...))))
and one has a sequence {rn} then one can define
fr(x) =
1/(a1+r1/(a2+r2/(a3+r3/(a4+ ...)))).
Another way of combing is to create a different function
gr(x) =
1/(a1r1+1/(a2r2+1/(a3r3+1/(a4r4+ ...)))).
Note that these transformations may not be well defined when x is
irrational; however, whenever x is rational, then the continued fraction
has a finite number of terms, and the operations are always well
defined.
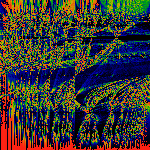
Cmap
Cosine Transform fr(x) with rn=cos(nz). Parameter
z runs from zero at the bottom, to 2pi at the top.
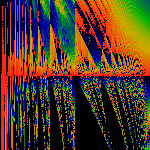
Emap
Exponential Transform fr(x) with rn=exp(-nt).
Parameter t runs from one at the bottom to minus one at the top.

Jmap
Spherical Bessel (j0) Transform
rn=j0(nz)
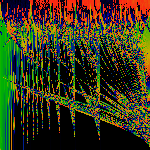
Cn
Sine Squared Transform rn=(1+cos(nz)). The goal here is to
avoid the pathological divide-by-zero's that occur in
Cmap when cos(nz) = -1. As is clear here, the figure
is far better behaved than Cmap.
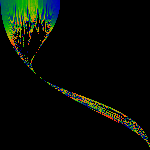
Magic Third
As above, except only the range 1/2 < x < 2/3 is shown (not to scale).
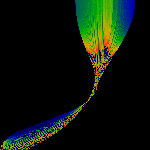
The Brush
A different 1/2 < x < 2/3 map.

Road to the Horizon
If x =
1/(a1+1/(a2+1/(a3+1/(a4+ ...))))
then consider
hg(x) =
1/(g(a1)+1/(g(a2)+1/(g(a3)+1/(g(a4)+ ...))))
In the road to the horizon, we use g(z)=1/z
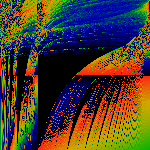
Phat
A 'trivial' reworking of the map: this shows x fz(x). Note
since f1(x) = x, that the bottom row of pixels is just
x2.
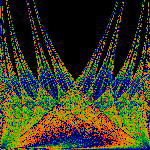
Crystalline
An attempt to create a symmetrized version.

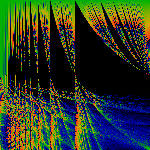

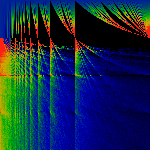
These show the basic map on an extended range ... either wider (x runs
zero to two) or taller (z runs zero to 4), or both. Note that we
accidentally flipped some of these "upside down".
Continued Crunch
These pictures depict the actual values that the function ranges over.
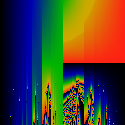

 The basic map, which is combined with itself to
show the symmetric and the anti-symmetric components.
The color at pixel (x,z) is simply the value of the
fz(x) mod 1.
Again, black=0.0, red=1.0, and a spectrum from blue to green in between.
Note that z runs from +1 at the top, to -1 downwards. Thus, the top
edge of the first picture is simple the straight line
f1(x)=x.
The basic map, which is combined with itself to
show the symmetric and the anti-symmetric components.
The color at pixel (x,z) is simply the value of the
fz(x) mod 1.
Again, black=0.0, red=1.0, and a spectrum from blue to green in between.
Note that z runs from +1 at the top, to -1 downwards. Thus, the top
edge of the first picture is simple the straight line
f1(x)=x.
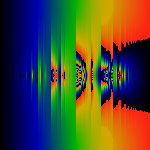
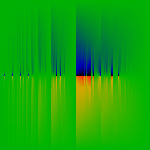 As above, but this time, z=eit with t running from 0 to 2pi bottom to
top. The first one shows the modulus, the second one the phase. Note how the phase
picture confirms the existence of the poles at z=-1.
The phases are colored with red=+pi, black=-pi, and green=0.
As above, but this time, z=eit with t running from 0 to 2pi bottom to
top. The first one shows the modulus, the second one the phase. Note how the phase
picture confirms the existence of the poles at z=-1.
The phases are colored with red=+pi, black=-pi, and green=0.
Glossary
- Farey Transform
- The term 'Farey Transform' is idiosyncratic on my part, I don't
believe anyone else calls it that (I don't know what they might call
it). I call it that because of its deep relationship to the
Farey Tree, as pointed out by John Conway.
The web page Gap Theory provides
a theoretical treatment in such a way that it becomes clear in what
ways these functions are well-defined, analytic, and etc.
- Hausdorff Measure
- When we say 'Hausdorff Measure' above, what we really mean is this:
Take the real number line between 0 and 1, and divide it into N equal
bins. We start with each bin being empty (zero).
Next, generate a sequence of random numbers 'x' between 0 and 1.
Apply a transform (f(x) mod 1) to each x. Then, if f(x) falls in the
i'th bin, increment the value of the i'th bin by one. When properly
normalized, the resulting 'density' on the real-number line converges
to a stable limit as
N is increased, and as the number of samples is increased. We loosely
call this value of the density the 'Hausdorff measure', in that it
describes a practical way of taking a well-defined limit.
Most of these images were generated during January and February of 1994,
in Austin, Texas. The work was inspired by a Christmas reading of
the "Contorted Fractions" chapter of John Conway's "On Numbers and Games".
The importance of Farey Trees to fractal phenomena was previously
brought to my attention by Paul Cvitanovi\'c during some lectures
in Paris in 1985.
Linas Vepstas February 1994
References
- Stern-Brocot
Tree
- Picture of a Farey Tree
- The
Rational
Mean as presented by Domingo Gómez Morín is a particularly
fascinating, forceful, and instructive
generalization of the ideas behind Farey addition.
It in turn leads to the concept of a
Rational
Process, which defines a set of sequences of ratios that
can be made to converge to ... well, I'm not sure ... not only the
golden mean, but also to any simple root ... seems like
these ideas might unify a variety of different concepts...
- The
Minkowski Question Mark provides another important bridge between
Farey Trees and Fractals.
-
Designing with Farey Fractions reviews how to weave Farey
Fractions into cloth! C'est fantastique!
The quickie bibliography below was scammed from
http://www.math.uwn.edu/Farey.html
- J.C. Lagarias and C. Tresser, A walk along the branches of the
extended Farey tree, IBM Jour. of Res. and Dev., v. 39, 1995.
- J.C. Lagarias, Number theory and dynamical systems, Proceedings
of Symposia in Applied Mathematics 46, 35-72, 1992.
- R. Siegel, C. Tresser, and G. Zettler, A decoding problem in
dynamics and in number theory, Chaos 2, 473-493, 1992.
- G.H. Hardy and E.M. Wright, An introduction to the theory
of numbers, fifth edition, Clarendon, Oxford, England, 1979.
- J. Farey, On a curious property of vulgar fractions, Philos.
Mag. & Journal, London 47, 385-386, 1816.
- Anonymous author, On vulgar fractions, Philos. Mag. &
Journal, London 48, 204, 1816.
- J. Farey, Propriété curieuse des Fractions
Ordinaires, Bull. Sc. Soc. Philomatique 3, No. 3, 112, 1816.
- J. Franel, Les Suites de Farey et le Problémes des
Nombres Premiers, Gottinger Nachrichten, pp. 198-201, 1924.
- P. Cvitanovi\'c, Farey Organization of the fractal hall effect,
Phys. Scripta T9, 202, 1985.
- P. Cvitanovi\'c, B. Shraiman, and B. Söderberg, Scaling
laws for mode locking in circle maps, Phys. Scripta 32, 263-270, 1985.
Copyright (c) 1994 Linas Vepstas All Rights Reserved.

The Farey Room
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.









 The basic map, which is combined with itself to
show the symmetric and the anti-symmetric components.
The color at pixel (x,z) is simply the value of the
fz(x) mod 1.
Again, black=0.0, red=1.0, and a spectrum from blue to green in between.
Note that z runs from +1 at the top, to -1 downwards. Thus, the top
edge of the first picture is simple the straight line
f1(x)=x.
The basic map, which is combined with itself to
show the symmetric and the anti-symmetric components.
The color at pixel (x,z) is simply the value of the
fz(x) mod 1.
Again, black=0.0, red=1.0, and a spectrum from blue to green in between.
Note that z runs from +1 at the top, to -1 downwards. Thus, the top
edge of the first picture is simple the straight line
f1(x)=x.

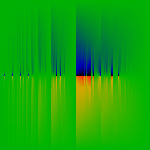 As above, but this time, z=eit with t running from 0 to 2pi bottom to
top. The first one shows the modulus, the second one the phase. Note how the phase
picture confirms the existence of the poles at z=-1.
The phases are colored with red=+pi, black=-pi, and green=0.
As above, but this time, z=eit with t running from 0 to 2pi bottom to
top. The first one shows the modulus, the second one the phase. Note how the phase
picture confirms the existence of the poles at z=-1.
The phases are colored with red=+pi, black=-pi, and green=0.
