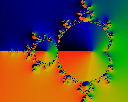
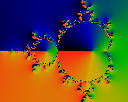
Because Z'n has a high 'rotation', it is handier to deal with
the normalized vector Pn = Z'n/Zn
Here we graph the phase
phi=arctan (Re Pn / Im Pn).
Note that not all buds are
alike: the interior of some buds see a full rotation of the phase by
360 degrees; others do not.

Very curiously, this seems to depend on the
factorization of the loop termination count. When the loop termination
count is prime, none of the buds rotate; when it is a product of many
small (repeated) factors, most buds rotate. For example, in this
image, most buds rotate because iteration was stopped at 1260=4*9*5*7,
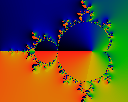
whereas this image stopped at 1259 (which is a prime number) and
none of the buds rotate.
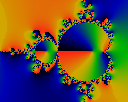
The phase of the second normalized derivative Qn = Z''n/Zn where Z''n+1 = 2 * (Zn * Z''n + Z'2n)
Iterated to a high order (N=4153) before stopping.
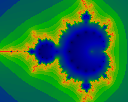
Same image as above, but iterated to only N=19. Note the presence of
'zeros' (black dots) on the interior, which are missing from the
high-iteration image.
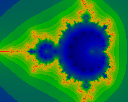
As above, but iterated to N=18. Note that this image contains one less
black dot on the belt.
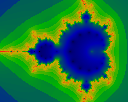
Iterated to N=17. Notice how the images generated with prime N are
subtly different than those with composite iteration counts.
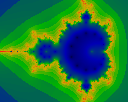
Iterated to N=16. Note that 18 is divisible by 3, while 16 is not: thus the large bud has a green dot in the middle, but the next-smaller one doesn't (unlike the N=18 case).
In this image, black is zero, moving
through blue, green, yellow to a red of 1.0.

Note the Moire patterning make it difficult to discern where the actual limit is. To eliminate this, this image was iterated only to N=50, and so we can see the limit-circle at 50 dots.
This first picture shows the iteration to n=9. (We've dropped the factor
of log 2).
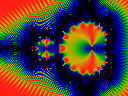
Iterate to n=2520=8*9*5*7 a product of small primes.
Oddly, the n=2 bulb is unlit, but n=3 and so on light up.
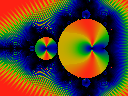
Iterate to n=2519 which is a prime number. Oddly, the n=2 bud lights up, the none of the other buds do. Thus, the counting rules here seem to be a bit different than one might expect ...
This image shows |z| / |z|'.
Copyright (c) 1997, 2000 Linas Vepstas

M-Set Derivatives
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.