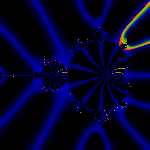
 The 1/15 and 2/15 rays (in red) surrounding the m(1/4) bud.
The 1/15 and 2/15 rays (in red) surrounding the m(1/4) bud.
Visually, the stuff here is pretty boring. Don't expect any hot graphics. The interesting part on this page is the relationship between arc-angles and features. The Parameter Rays page describes how the rays are computed and numbered, while a mathematical intro is given on the Douady-Hubbard Potential page.
 The 1/15 and 2/15 rays (in red) surrounding the m(1/4) bud.
The 1/15 and 2/15 rays (in red) surrounding the m(1/4) bud.
 The 1/31 and 2/31 rays (in red) surrounding the m(1/5) bud.
The 1/31 and 2/31 rays (in red) surrounding the m(1/5) bud.
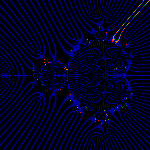 The 17/127 and 18/127 rays (in red) surrounding the m(2/7) bud.
Note that the 2/7'ths bud is in the middle (via Farey addition)
between 1/3 and 1/4.
The 17/127 and 18/127 rays (in red) surrounding the m(2/7) bud.
Note that the 2/7'ths bud is in the middle (via Farey addition)
between 1/3 and 1/4.
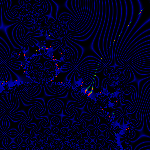 The 273/2047 and 274/2047 rays (in red) surrounding the m(3/11) bud.
Note that the 3/11 bud is in the middle (via Farey addition)
between 2/7 and 1/4.
The 273/2047 and 274/2047 rays (in red) surrounding the m(3/11) bud.
Note that the 3/11 bud is in the middle (via Farey addition)
between 2/7 and 1/4.
 Here's a picture of the 4/15 bud, with the rays
[4369/32767, 4370/32767] pointing at its base
highlighted in red.
Its quite small.
Recall 4/15'ths position on the Farey tree:
[1/3 2/7 3/11 4/15 1/4] i.e.
to the right(4/15) to the right(3/11) of
the one in the middle(2/7) between 1/3 and 1/4.
Here's a picture of the 4/15 bud, with the rays
[4369/32767, 4370/32767] pointing at its base
highlighted in red.
Its quite small.
Recall 4/15'ths position on the Farey tree:
[1/3 2/7 3/11 4/15 1/4] i.e.
to the right(4/15) to the right(3/11) of
the one in the middle(2/7) between 1/3 and 1/4.
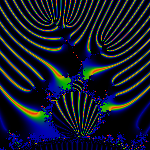 Rays at inverse powers of two touch the tips of the prominent
antennas of the m(1/3) bud.
Rays at inverse powers of two touch the tips of the prominent
antennas of the m(1/3) bud.
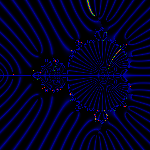 The 1/4 ray (in red) landing at the tip of the antenna of the m(1/3) bud.
The 1/4 ray (in red) landing at the tip of the antenna of the m(1/3) bud.
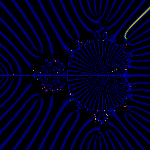 The 1/8 ray (in red) landing at the tip of the antenna of the m(1/4) bud.
The 1/8 ray (in red) landing at the tip of the antenna of the m(1/4) bud.
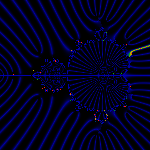 The 1/16 ray (in red) landing at the tip of the antenna of the m(1/5) bud.
The 1/16 ray (in red) landing at the tip of the antenna of the m(1/5) bud.
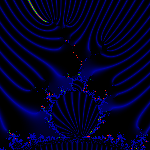 A closeup of the 1/4 ray touching the tip of the
antenna of the m(1/3) bud.
A closeup of the 1/4 ray touching the tip of the
antenna of the m(1/3) bud.
A theoretical treatment is given by Devaney, Moreno-Rocha, Geometry of the Antennas in the Mandelbrot Set (or mirror here)
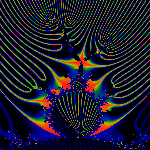
 The bifurcation of the antenna at [9, 11, 15] / 56 on the m(1/3) bud.
The bifurcation of the antenna at [9, 11, 15] / 56 on the m(1/3) bud.
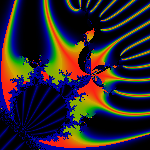 The trifurcation of the antenna at [17, 19, 23, 31] / 240 on
the m(1/4) bud. Note the artifacts, these are discussed on the
ray page.
The trifurcation of the antenna at [17, 19, 23, 31] / 240 on
the m(1/4) bud. Note the artifacts, these are discussed on the
ray page.
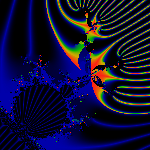 How can we be sure of the above fractions? Here, we split the
17/240 and 31/240 rays down the middle. We can see clearly
bow the red edge points at the quadrifurcation.
How can we be sure of the above fractions? Here, we split the
17/240 and 31/240 rays down the middle. We can see clearly
bow the red edge points at the quadrifurcation.
 The quadri-furcation of the antenna at [33, 35, 39, 47,63] / 992 on
the m(1/5) bud. Note the artifacts, these are discussed on the
ray page.
The quadri-furcation of the antenna at [33, 35, 39, 47,63] / 992 on
the m(1/5) bud. Note the artifacts, these are discussed on the
ray page.
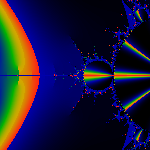 The mono-furcation of the antenna at the end of the m(1/2) bud
isn't at all obvious, because, well, there's no obvious visual signpost.
However, the formula tells us its at [5,7]/12. We've colored here so
that the sharp red edge points exactly at it.
The mono-furcation of the antenna at the end of the m(1/2) bud
isn't at all obvious, because, well, there's no obvious visual signpost.
However, the formula tells us its at [5,7]/12. We've colored here so
that the sharp red edge points exactly at it.
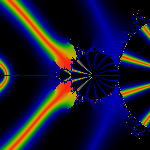 The primary bud due west of the m(1/2) bud is separated by [2,3]/5
and thus has a period q=4 with cycle (2,4,3,1).
The primary bud due west of the m(1/2) bud is separated by [2,3]/5
and thus has a period q=4 with cycle (2,4,3,1).
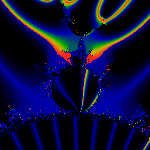 The primary buddy of m(1/3) is split off by [10,17]/63,
and has a period q=6 with cycle (10,20,40,17,34,5)
The primary buddy of m(1/3) is split off by [10,17]/63,
and has a period q=6 with cycle (10,20,40,17,34,5)
 The primary buddy of m(1/4) is split off by [18,33]/255,
and has a period q=8 with cycle (18,36,72,144,33,66,132,9)
The primary buddy of m(1/4) is split off by [18,33]/255,
and has a period q=8 with cycle (18,36,72,144,33,66,132,9)
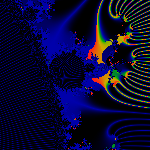 The primary buddy of m(1/5) is split off by [34,65]/1023,
and has a period q=10 with cycle (34,68,136,272,544,65,130,260,520,17)
The primary buddy of m(1/5) is split off by [34,65]/1023,
and has a period q=10 with cycle (34,68,136,272,544,65,130,260,520,17)
In the limit, this appears to converge to 0.412454033640107 which is the Thue Morse codeword. Its not obvious to me why it appears here; but I haven't thought about it either. (See, for example, Thue Morse L-systems for its relevance to fractals. See also A Fresh Look at Number for the occurrence of complimentary (gray-code) Thue-Morse in the symbolic dynamics of the logistic equation.) The codeword is the Farey number of 0.418979789366342 but this number seems to be unknown.
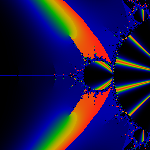 The primary bud due west of the m(1/2) bud is separated by [2,3]/5
and thus has a period q=4 with cycle (2,4,3,1).
The primary bud due west of the m(1/2) bud is separated by [2,3]/5
and thus has a period q=4 with cycle (2,4,3,1).
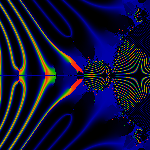 The bud due west of the bud due west is rayed by [7,10]/17
and thus has a period q=8 with cycle (7,14,11,5,10,3,6,12).
The bud due west of the bud due west is rayed by [7,10]/17
and thus has a period q=8 with cycle (7,14,11,5,10,3,6,12).
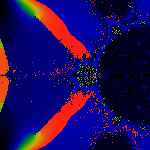 The bud due west ... is rayed by [106,151]/257
and thus has a period q=16 with cycle
(106,212,167,77,154,51,102,204,151,45,90,180,103,206,155,53)
The bud due west ... is rayed by [106,151]/257
and thus has a period q=16 with cycle
(106,212,167,77,154,51,102,204,151,45,90,180,103,206,155,53)
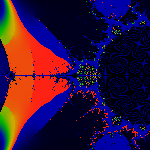 The bud due west ... is rayed by [27031,38506]/65537
The bud due west ... is rayed by [27031,38506]/65537
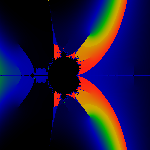 The two rays entering its tail are 3/7 and 4/7. It has period q=3.
The two rays entering its tail are 3/7 and 4/7. It has period q=3.
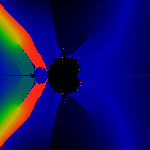 The two rays splitting off the primary bud are 4/9 and 5/9.
The bud has period q=6, that is, twice the period of the mini-cardiod.
The two rays splitting off the primary bud are 4/9 and 5/9.
The bud has period q=6, that is, twice the period of the mini-cardiod.
In general, the rays that go into the tails of mini-me's seem to be of the for p/(2n-1) for some integers p, n. The following pictures show some of these. Unfortunately, they are quite messy, because the ray algorithm breaks down in this area. As mentioned elsewhere, there doesn't seem to be any way f fixing this algorithm, and I don't know of others.
 This one shows the rays 3/31 and 4/31. The 3/31 ray is the red-blue
discontinuity coming in from the right side, and heading straight into
the tail of the bud. The 4/31 ray comes in from the left, gets
interfered with by the busted algorithm but if you look at it just
right, you'll see that it goes into the tail as well. This mini-me is
the largest one on the longest antenna spoke of the 1/4 bud.
This one shows the rays 3/31 and 4/31. The 3/31 ray is the red-blue
discontinuity coming in from the right side, and heading straight into
the tail of the bud. The 4/31 ray comes in from the left, gets
interfered with by the busted algorithm but if you look at it just
right, you'll see that it goes into the tail as well. This mini-me is
the largest one on the longest antenna spoke of the 1/4 bud.
 The [5,6]/31 rays from a distance.
The [5,6]/31 rays from a distance.
 The same view, using ordinary coloration. So which mini-me was that?
Why, the largest one on the smaller antenna of the 1/3 bud.
The same view, using ordinary coloration. So which mini-me was that?
Why, the largest one on the smaller antenna of the 1/3 bud.
There seems to be a pattern, but its hard to describe & intuit.
For example,
the [7,8]/31 rays enter the tail of the largest mini-me on the longest
antenna of the largest mini-me of the 1/3 bud. The [9,10]/31 rays pinch
off the 2/5 bulb, while the [11,12]/31 rays go to the tail of the
mini-off-the-mini-off-the 1/2 bud.