Logistic Equation Variations

The colors represent Poincare Recurrance times for omega along the horizontal axis, and lambda along the vertical axis. Remember -- click on the small image to get a big view.

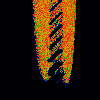
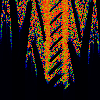
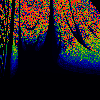From left to right:

Sin: x[n+1] = lambda * sin (pi * (x[n]-omega)) mod 1
Gauss: x[n+1] = lambda * exp (pi * (x[n]-omega)^2) mod 1
Sinc: x[n+1] = lambda * sinc (pi * (x[n]-omega)) mod 1 where sinc(y) = sin(y) / y
Expand: Let y = x[n] - 1/ (omega-0.5) and z = x[n] + 1/ (omega-0.5) Then x[n+1] = lambda * y * z

Expansions and Distortions

All of the below represent the standard logistic equation; they differ merely in the coordinate mapping. That is, they are really the same picture, just distorted.

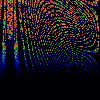
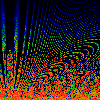
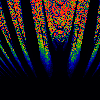From left to right:

Squash: y = x[n] - omega, z = x[n] + omega, x[n+1] = lambda * y * (1-z) mod 1
Flip: y = x[n] - omega, z = x[n] + omega, x[n+1] = (1/lambda) * y * (1-z) mod 1
Sku: y = x[n] - (omega-0.5)/lambda + 0.5
z = x[n] + (omega-0.5)/lambda + 0.5
x[n+1] = y * (1-z) mod 1

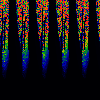
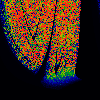From left to right:

Squirt: y = x[n] - (omega-0.5)/sqrt(lambda) + 0.5
z = x[n] + (omega-0.5)/sqrt(lambda) + 0.5
x[n+1] = y * (1-z) mod 1
Stret: y = x[n] - sqrt (omega / lambda) + 0.5
z = x[n] + sqrt (omega / lambda) + 0.5
x[n+1] = y * (1-z) mod 1
Tch: Same equation as Stret, different domain.

Logistic Equation Variations by Linas Vepstas is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.