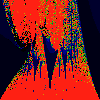Poincarre Recurrance Time for Damped Circle Map
Basically,
x(n+1) = x(n) + omega + K * sin (2 * PI * x(n))
is the circle map. This page explores complex K. (Ohh,
and be sure to visit the Movie Room
to see MPEG movies of related phenomena).
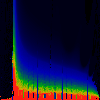
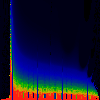
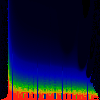
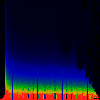
In each of the pictures below, we have omega on the x-axis, running from
0.0 too 1.0. Along the y-axis, we have mag|K|, from 0.0 to 3.0.
In the first series below, the phase of K runs from zero to 1.6, in steps of
0.1.
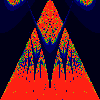
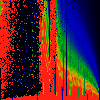
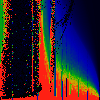
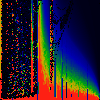
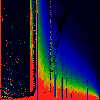
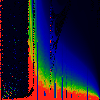
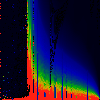
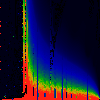
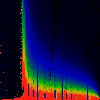
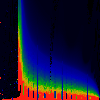
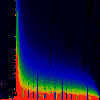
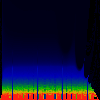
As above, but phase of K runs from 0.0 to 0.1, in steps of 0.01
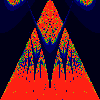
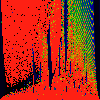
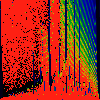
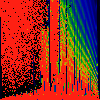
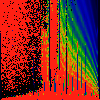
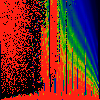
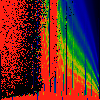
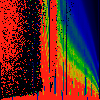
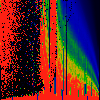
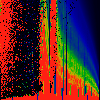
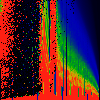
As above, but phase of K runs from 0.0 to 0.01, in steps of 0.001
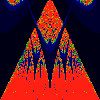
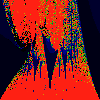
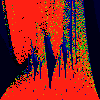
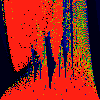
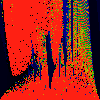
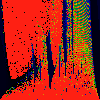
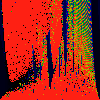
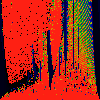
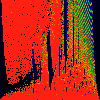
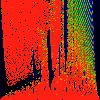
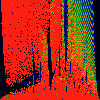
As above, but phase of K runs from 0.0 to 0.001, in steps of 0.0001
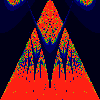
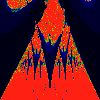
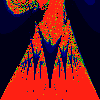
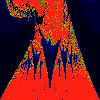
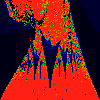
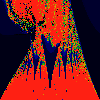
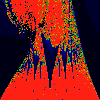
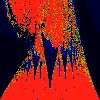
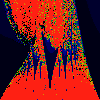
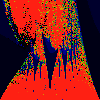
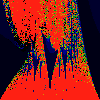
As above, but phase of K is 0.0004 -- basically, a blow up of fifth
image above.
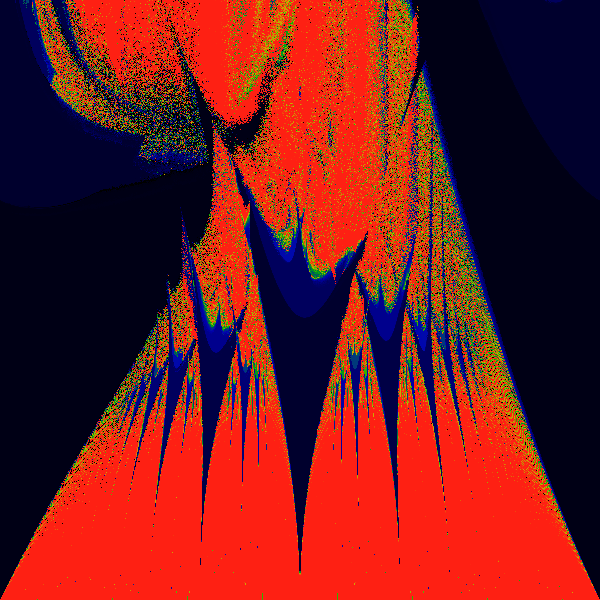
And now, some monsters -- this one has K pure imaginary. Again, K=0.0 to
3.0 along y-axis, and omega 0.0 to 1.0 along x-axis.
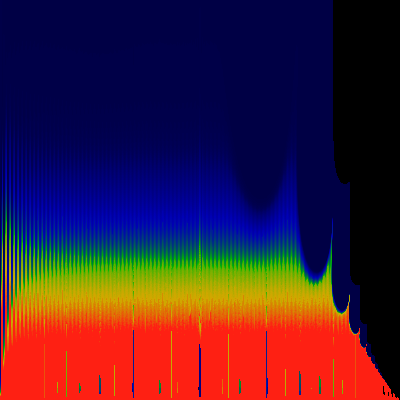
Again one has K pure imaginary. Again, K=0.0 to
1.5 along y-axis, and omega 0.0 to 0.51 along x-axis.
Gee, what's that ringing?
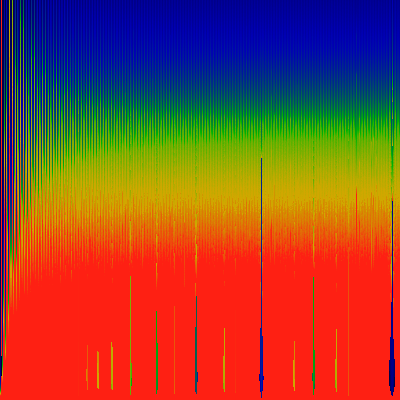
Again one has K pure imaginary. Again, K=0.0 to
1.5 along y-axis, and omega 0.0 to 0.126 along x-axis.
Are the apperent oscillations a numerical
artifact? or are they real ???
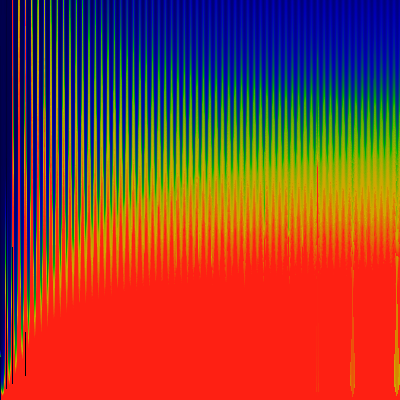
Again one has K pure imaginary. Again, K=0.0 to
1.5 along y-axis, and omega 0.100 to 0.106 along x-axis.
Note that the "epsilon" used to determine if we've
recurred back to the same spot is 0.002.
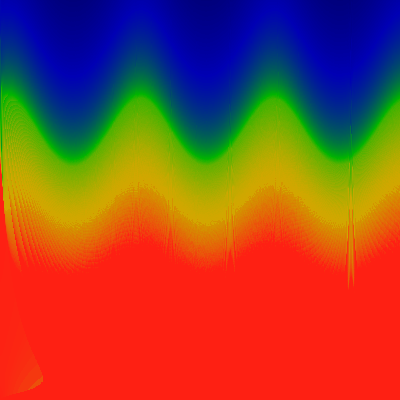
Again one has K pure imaginary. Again, K=0.0 to
1.5 along y-axis, and omega 0.100 to 0.106 along x-axis.
The difference is that here, the "epsilon" used to determine if we've
recurred back to the same spot is 0.0004.
Note that the features ARE independent of the epsilon.
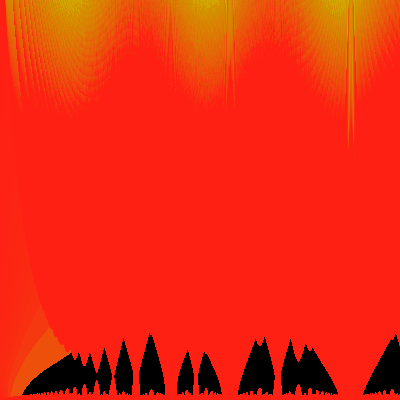
Note that the period of one oscillation is 1/500. Well, you might not
guess this, but ... an iteration of the equation is allowed to "settle
down" for some number of cycles, to get rid of transients, before we
measure the recurrance time. Well ... in this case, the equation was
allowed to settle for 500 iterations.
Changeing this settling time to 800 iterations yeilds the picture
below...
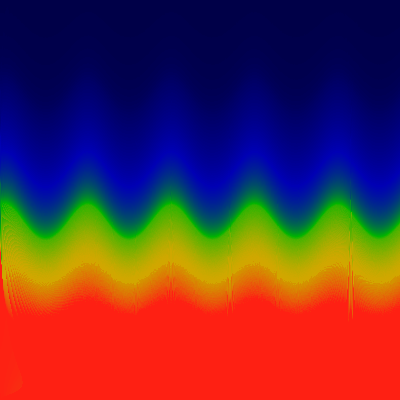
Well, I guess that settles it. It's a real artifact.
Copyright (c) 1995 Linas Vepstas

Damped Circle Map
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.