The Circle Period
This page explors the iterated circle map, aka 'kicked rotor',
xn+1 =
xn + omega - K * sin (2 * PI * xn)
for 0 < omega < 1 and positive K.
This iterated equation is a crude model for a kicked rotating disk.
It also roughly describes mode locking in a phase-locked loop (PLL)
electronic circuit.
For small-medium values of K and many values of omega, iteration
promptly converges onto a fixed point. The regions of K and omega
where iteration converges to a fixed point are the 'mode-locked'
areas of the phase-locked loop, and appear black in the graphs
below. To students of chaotic dynamics, these black regions are
known as 'Arnold's Tongues'.
The top three graphs show the winding number nu=xn/n,
as a function of omega (along the horizontal) and K (along the
vertical). Nu can be thought of as the 'speed' of the spinning disk:
At the fastest speed, nu=1, i.e. Xn incremented by nearly 1
nearly every iteration. These are shown in red. Lower winding numbers
are spread across a spectrum from red through orange, yellow, green,
blue, fading to black for nu=0. The mode locked regions are in black
because there, xn as converged to a fixed point, and is not
moving at all. Mode-locked regions seem to occur near all rational
numbers, and seem to intertwine in a self-similar way. Note how the
'tongues' bear some superficial resemblance to certain
manipulations of continued fractions.
The tall graph, omega runs from 0 to 1 horizontally, and K runs
from 0 to 3 vertically. The other graphs are enlargements of
interesting sub-pieces. Click on the images to see a larger view.



Two views of the same dataset. Both show Poincare recurrance times.
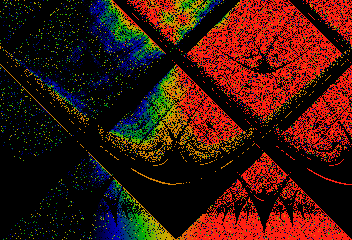
Logarithm of the above.

(Data allowed to settle 500 cycles before counting started.
Iteration stopped after 20,000 iterations. Epsilon for poincare
recurrance times was 1.3e-5)
The top figures were originally created in 1990 and 1991. The bottom
frames are from a movie created in 1996.
Copyright (c) 1990, 1991, 1996 Linas Vepstas

The Circle Period
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.





