Peatüki algus: Maatriksi Jordani kuju
Eelmine: Maatriksi Jordani kuju analüüs
Järgmine: Lineaarsete algebraliste võrrandisüsteemide lahendamise otsesed meetodid

Kui n=1, siis Jordani kast langeb ühte antud maatriksiga ja valem (9) on tõene. Oletame, et maatriksi A Jordani kasti konstruktsiooni valemite (9) abil on leitud kui maatriksi A järk on väiksem kui n. Kasutame matemaatilise induktsiooni meetodit.

I samm. Kui eeldada, et A on singulaarne, siis Vaadeldes vastavat maatriksit, on selle korral konstruktsioon valemite (9) abil teostatav. Nimelt, ruumis leidub r sõltumatut sellist vektorit , et nende korral peavad paika seosed
 

II samm. Oletame, et Iga nullruumi vektor on maatriksi A omavektor, mis vastab maatriksi A omaväärtusele Seepärast peab sammul I olema p ahelat, mis algavad omaväärtusele 0 vastava omavektoriga. Meid huvitab iga sellise ahela viimane vektor. Kuna need alamruumi kuuluvad vektorid peavad kuuluma ka ruumi siis nad peavad olema maatriksi A veeruvektorite lineaarkombinatsioonid

mingi korral. Järelikult vektor järgneb vektorile omaväärtusele vastavas ahelas.

III samm. Kuna siis peab leiduma veel n-r-p lineaarselt sõltumatut ruumi vektorit alamruumi ortogonaalses täiendis.

Lause 5.3.1. Filipovi algoritm määrab r vektorit p vektorit ja n-r-p vektorit mis määravad Jordani ahelad. Need vektorid on lineaarselt sõltumatud ja sobivad maatriksi X veeruvektoreiks ning J=X^-1AX.

Tõestus. Vaadake Strang (1988, lk 457).

Näide 5.3.1. Leiame maatriksi

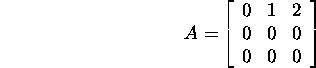
Jordani normaalkuju, kasutades Filipovi algoritmi.

I samm. Maatriksi kujust on näha, et ja Seega r=1 ja leidub tingimust (10) rahuldav vektor sellest alamruumist

II samm. Leiame maatriksi A nullruumi baasi:

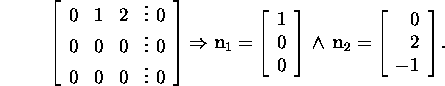
Vektor kuulub alamruumi ja Lahendame süsteemi

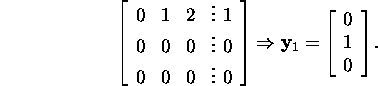
III samm. Valime vektoriks vektori
''Kleebime'' kokku maatriksi X:

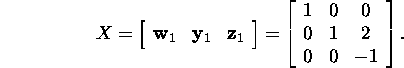
Leiame pöördmaatriksi



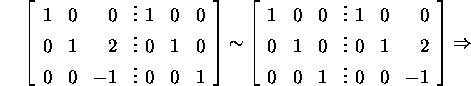
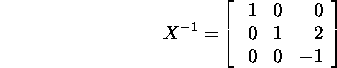
ja Jordani maatriksi

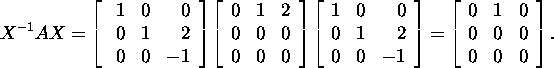
Pakett ''Maple'' pakub Jordani lahutuseks:

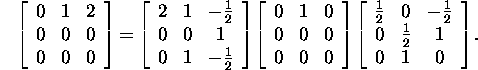
Kuna maatriksi A Jordani lahutuses esinev maatriks X pole üheselt määratud, siis paljude ülesannete korral pakub huvi valida maatriks X nii, et konditsiooniarv k(X) oleks minimaalne. Selline probleem tekkis ka näite 1.2.9.4 lahendamisel.

Ülesanne 5.3.1. Leidke maatriksi

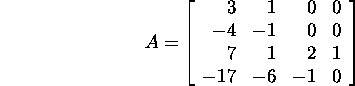
Jordani lahutus.

Ülesanne 5.3.2.^* Leidke maatriksi

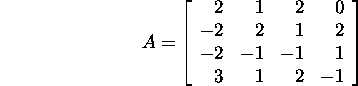
Jordani lahutus.

Ülesanne 5.3.3.^* Leidke maatriksi

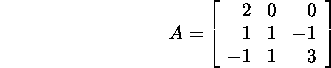
Jordani lahutus.

Ülesanne 5.3.4. Olgu maatriksi Jordani lahutus kujul A=MJM^-1. Näidake, et .

Peatüki algus: Maatriksi Jordani kuju
Eelmine: Maatriksi Jordani kuju analüüs
Järgmine: Võrrandisüsteemide lahendamine iteratsioonimeetodil