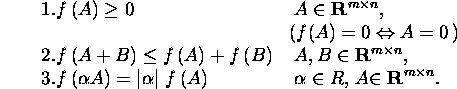
Maatriksi normi tähistatakse
Peatüki
algus: Maatriksid
Eelmine: Schuri lahutus
Järgmine: Cayley-Hamiltoni
teoreem
Definitsioon 2.7.1. Kujutust
![]() nimetatakse maatriksi normeerimiseks ja saadud väärtusi
maatriksi normiks, kui on täidetud järgmised kolm tingimust:
nimetatakse maatriksi normeerimiseks ja saadud väärtusi
maatriksi normiks, kui on täidetud järgmised kolm tingimust:
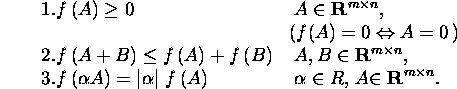
Maatriksi normi tähistatakse ![]()
Lineaaralgebras on enamkasutatavateks maatriksi normideks
Frobeniuse norm,
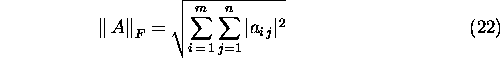
ja p-normid ![]()
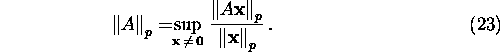
Valemist (23) järeldub, et
![]()
ehk
![]()
Kontrollime p-normi korral maatriksi
normi tingimuste täidetust. Leiame, et
![]()
![]()
![]()
![]()
ja
![]()
![]()
![]()
ning
![]()
![]()
Ülesanne 2.7.1. Kontrollige Frobeniuse normi korral maatriksi normi tingimuste täidetust.
Ülesanne 2.7.2.* Arvutage
maatriksi A Frobeniuse norm ![]() kui
kui
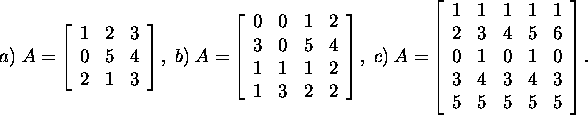
Definitsioon 2.7.2. Fikseeritud
maatriksi normi korral regulaarsele ruutmaatriksile ![]() vastavaks konditsiooniarvuks nimetatakse suurust
vastavaks konditsiooniarvuks nimetatakse suurust
![]()
Frobeniuse normile vastavat konditsiooniarvu
tähistatakse kF(A) ja p-normile
vastavat konditsiooniarvu tähistatakse kp(A).
Singulaarse ruutmaatriksi ![]() korral defineeritakse
korral defineeritakse ![]()
Ülesanne 2.7.2. Näidake, et kui
![]() siis
siis
![]()
![]()
![]()
Lause 2.7.1. Normi
![]() leidmise eeskiri (23) on teisendatav kujule
leidmise eeskiri (23) on teisendatav kujule
![]()
Tõestus. Kasutades normi
kolmandat omadust ja homogeensust vektori korrutamisel maatriksiga, saame
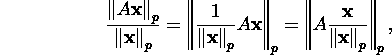
kusjuures 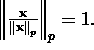
Lause 2.7.2. Kui ![]() ,
,
![]() ja
ja ![]() siis
siis ![]()
Tõestus. Seoste (24) ja
(25) abil leiame, et
![]()
![]()
Märkus 2.7.1. Et ![]() siis alati
siis alati ![]() .
.
Märkus 2.7.2. Iga ![]() ja
ja ![]() korral ning suvalise vektori normi
korral ning suvalise vektori normi 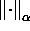 korral ruumis
korral ruumis ![]() ja
ja ![]() korral ruumis
korral ruumis ![]() peab paika seos
peab paika seos
![]()
kusjuures maatriksi norm ![]() on defineeritud valemiga
on defineeritud valemiga
![]()
Kuna hulk ![]() on kompaktne ja
on kompaktne ja ![]() on pidev, siis
on pidev, siis
![]()
kusjuures ![]() ja
ja ![]()
Definitsioon 2.7.3. Kui k(A) on suhteliselt väike, siis maatriksit A nimeta-takse hea konditsiooniga maatriksiks, kui aga k(A) on suur, siis halva konditsiooniga maatriksiks.
Definitsioon 2.7.4.
Ruutmaatriksi A normi ![]() nimetatakse
kooskõlas olevaks vektori normiga
nimetatakse
kooskõlas olevaks vektori normiga ![]() kui
kui
![]()
ja ta on submultiplikatiivne, so
![]()
Definitsioon
2.7.5. Vektori normiga ![]() kooskõlas olevat ruutmaatriksi normi
kooskõlas olevat ruutmaatriksi normi
![]() nimetatakse
vektori normile
nimetatakse
vektori normile ![]() alluvaks, kui iga maatriksi A korral leidub selline vektor
alluvaks, kui iga maatriksi A korral leidub selline vektor
![]() et
et ![]()
Lause 2.7.3. Suvalise vektori normi ![]() korral leidub vähemalt üks selle vektori
normile alluv (seepärast ka vähemalt üks vektori
normiga kooskõlas olev) maatriksi norm
korral leidub vähemalt üks selle vektori
normile alluv (seepärast ka vähemalt üks vektori
normiga kooskõlas olev) maatriksi norm ![]() ja nimelt
ja nimelt
![]()
Märkus 2.7.3. Mitte kõik maatriksi
normid ei rahulda submultiplikatiivsuse omadust ![]() .
Näiteks normi
.
Näiteks normi
![]()
ja maatriksite
![]()
korral ![]() ning
ning
![]()
Lause 2.7.4. Kui ![]() ,
siis kehtivad maatriksi normide vahelised järgmised seosed:
,
siis kehtivad maatriksi normide vahelised järgmised seosed:
![]()
![]()
![]()
![]()
![]()
![]()
Kui ![]() ja
ja ![]() siis
siis
![]()
Tõestame valemi (27).
Leiame, et
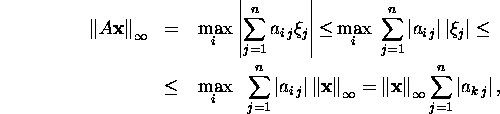
kusjuures maksimum olgu saadud indeksi i väärtuse
k korral. Saame hinnangu
![]()
Olgu
![]()
ja
![]()
Kuna ![]() siis
siis
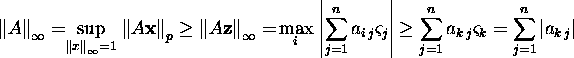
ning seega
![]()
Näide 2.7.1. Leiame maatriksi A normid
![]() ja
ja ![]() , kui
, kui
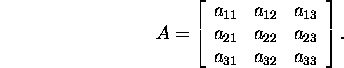
Seostest (26) ja (27) leiame, et
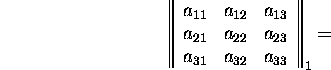
![]()
ja
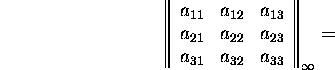
![]()
Näide 2.7.2. Leiame maatriksi A pöördmaatriksi
A-1 ja nende normid ![]()
![]()
![]() ning maatriksi A konditsiooniarvud
k1(A),
ning maatriksi A konditsiooniarvud
k1(A), ![]() , kui
, kui
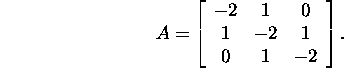
Saame, et
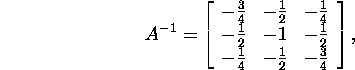
![]()
ja
![]()
Kui valemid (26) ja (27)
võimaldavad lihtsalt arvutada vastavalt 1-normi
ja ![]() -normi,
siis 2-normi arvutamine on keerukam. Maatriksi
2-normi nimetatakse ka maatriksi spektraalnormiks.
-normi,
siis 2-normi arvutamine on keerukam. Maatriksi
2-normi nimetatakse ka maatriksi spektraalnormiks.
Lause 2.7.5. Kui ![]() siis
siis
![]()
st ![]() on ruutjuur maatriksi ATA suurimast omaväärtusest.
on ruutjuur maatriksi ATA suurimast omaväärtusest.
Tõestus. Normi ![]() leidmiseks leiame esiteks
leidmiseks leiame esiteks ![]() Seega,
Seega,
![]()
Olgu ![]() Maatriks B on sümmeetriline maatriks, sest
Maatriks B on sümmeetriline maatriks, sest
![]()
ja
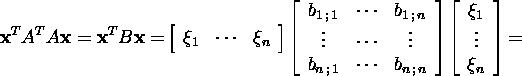
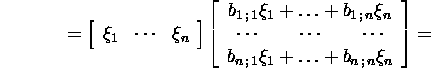
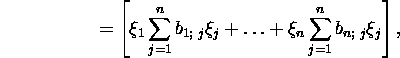
![]()
siis ![]() on n muutuja
on n muutuja ![]() funktsioon ning
funktsioon ning
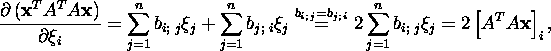
![]()
Ülesande, leida ![]() korral
on tegemist tingliku ekstreemumi leidmise ülesandega. Selle lahendamiseks
moodustame abifunktsiooni
korral
on tegemist tingliku ekstreemumi leidmise ülesandega. Selle lahendamiseks
moodustame abifunktsiooni
![]()
Funktsiooni ![]() statsionaarsete punktide leidmiseks koostame võrrandisüsteemi:
statsionaarsete punktide leidmiseks koostame võrrandisüsteemi:
![]()
st
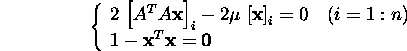
ehk
![]()
Seega iga statsionaarne punkt tingliku ekstreemumi jaoks on maatriksi ATA
omaväärtusele
vastav normeeritud vektor ![]() .
Avaldame seosest
.
Avaldame seosest ![]()
![]() omaväärtuse
omaväärtuse ![]() Saame, et
Saame, et ![]() ,
kusjuures
,
kusjuures ![]() Võrreldes saadud tulemust lähtevalemiga
Võrreldes saadud tulemust lähtevalemiga ![]() leidmiseks, näeme,et
leidmiseks, näeme,et ![]()
![]() .
Seega,
.
Seega,
![]()
st ![]() on ruutjuur maatriksi ATA suurimast omaväärtusest.
on ruutjuur maatriksi ATA suurimast omaväärtusest.
Järeldus 2.7.1. Kui maatriks ![]() on sümmeetriline, siis
on sümmeetriline, siis
![]()
Näide 2.7.3. Leiame maatriksi A pöördmaatriksi
A-1 ja nende normid ![]()
![]()
![]() ning maatriksi A konditsiooniarvud
k1(A),
ning maatriksi A konditsiooniarvud
k1(A), ![]() ,
kui
,
kui
![]()
Saame, et
![]()
![]()
Näide 2.7.4. Vaatleme, kuidas on seotud maatriksi
peaaegu singulaarsus (nullile lähedane determinandi
väärtus) ja maatriksi halb konditsioon.
Maatriksi
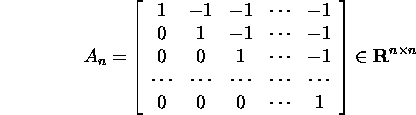
korral ![]() kuid
kuid ![]() Teisalt, diagonaalmaatriksi
Teisalt, diagonaalmaatriksi
![]()
korral kp(Dn)=1, kuid ![]() kuitahes väikese
kuitahes väikese ![]() korral.
korral.
Ülesanne 2.7.4.![]() Leidke maatriksi A pöördmaatriks A-1
ja nende normid
Leidke maatriksi A pöördmaatriks A-1
ja nende normid ![]()
![]() ning maatriksi A konditsiooniarvud
k1(A),
ning maatriksi A konditsiooniarvud
k1(A), ![]() ,
kui
,
kui
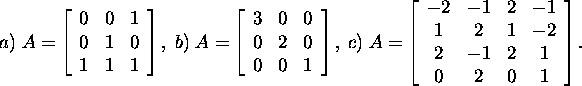
Peatüki
algus: Maatriksid
Eelmine: Schuri lahutus
Järgmine: Cayley-Hamiltoni
teoreem