Peatüki algus: Maatriksi Jordani kuju
Eelmine: Maatriksi diagonalisatsioon
Järgmine: Filipovi algoritm

Maatriksi Jordani maatriksi saamisel ei piisa maatriksi omaväärtuste leidmisest.

Näide 5.2.1. Leiame maatriksite

Jordani maatriksid J.

On lihtne veenduda, et maatriksite ja I spektrid on võrdsed:

Leiame neile vastavad omavektorid omaväärtuse korral:







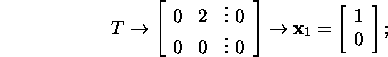
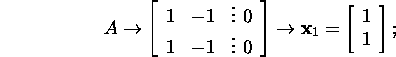
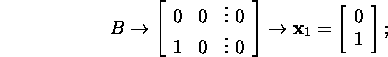
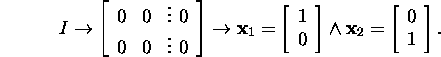
Näeme, et maatriksitel ja on vaid üks sõltumatu omavektor ja ainult üks omaväärtusele vastav Jordani kast ning maatriksitele ja vastab ühine Jordani maatriks

Maatriksil I on kaks lineaarselt sõltumatut omavektorit ja, järelikult, kaks Jordani kasti ja talle vastav Jordani maatriks ühtib maatriksiga I.

Ülesanne 5.2.1. Veenduge, et maatriksile

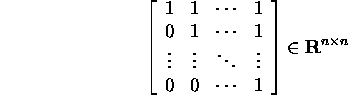
vastab üheblokiline Jordani maatriks

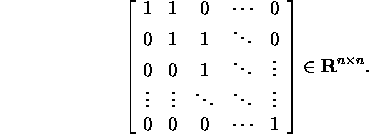
Näide 5.2.2. Uurime Jordani maatriksit
 
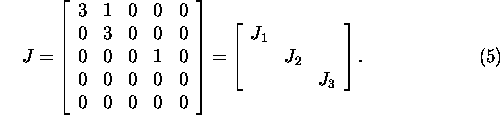
Leiame omaväärtusele mille kordsus on 2, vastavad omavektorid:

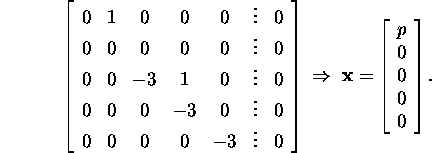
Järelikult vastab omaväärtusele üks lineaarselt sõltumatu omavektor ja üks Jordani kast

Leiame omaväärtusele mille kordsus on 3, vastavad omavektorid:

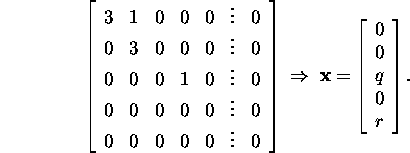
Seega omaväärtusele vastab kaks lineaarselt sõltumatut omavektorit ja ja kaks Jordani kasti,

ja

Kerkib küsimus, milliseid tingimusi peab suvaline maatriks A rahuldama, et talle vastavaks Jordani maatriks oleks seosega (5) antud maatriks Kuidas leida sellist regulaarmaatriksit X, et
 
Esimeseks nõudeks on tingimus kuid sellest ei piisa.Vaja on uurida ka maatriksi A omavektoreid. Esitame seose (6) kujul AX=XJ ehk

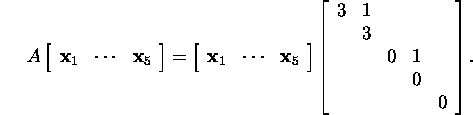
Korrutades maatriksid, saame valemid
 
ja
 
Valemitest (7) ja (8) järeldub, et sarnaselt maatriksiga J peab maatriksil A olema kolm omavektorit, ja Lisaks peab maatriksil A olema ka ks üldistatud omavektorit ehk kaks I järku lipuvektorit ja Öeldakse, et vektor kuulub ahelasse, mis algab vektoriga ja on määratud valemitega (7). See ahel määrab Jordani kasti J₁. Valemitest (8) kaks esimest määravad vektoritest ja koosneva teise ahela ning see ahel omakorda Jordani kasti J₂. Viimane valemitest (8) määrab vektorist koosneva kolmanda ahela ning see ahel omakorda Jordani kasti J₃.

Lause 5.2.1. Maatriksi Jordani kuju J määramine taandub ahelate otsimisele. Iga ahel algab maatriksi A omavektoriga ning igal indeksi i=1:n väärtusel
 
Vektorid on maatriksi X veeruvektorid ja iga ahel määrab ühe Jordani kasti.

Peatüki algus: Maatriksi Jordani kuju
Eelmine: Maatriksi diagonalisatsioon
Järgmine: Filipovi algoritm