Peatüki
algus: Maatriksid
Eelmine: Determinandid
Järgmine: Maatriksi
omaväärtused ja omavektorid
Vaatleme reaalarvulist ![]() maatriksit
maatriksit
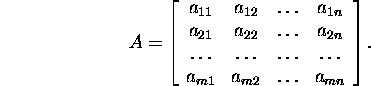
Maatriksit A on võimalik esitada nii maatriksi
A veeruvektorite ![]() =1:n)abil
kui ka maatriksi A transponeeritud reavektorite
=1:n)abil
kui ka maatriksi A transponeeritud reavektorite ![]() =1:m)
abil
=1:m)
abil
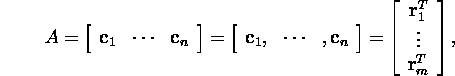
kusjuures ![]() ja
ja ![]() ning
ning 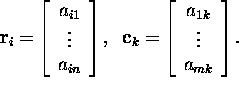
Definitsioon 2.4.1.
Maatriksi A veeruvektorite hulga ![]() lineaarset katet
lineaarset katet ![]() nimetatakse maatriksi A veeruvektorite alamruumiks ja tähistatakse
nimetatakse maatriksi A veeruvektorite alamruumiks ja tähistatakse
![]() või ran(A).
või ran(A).
Definitsioon 2.4.2.
Maatriksi A reavektorite hulga ![]() lineaarset katet nimetatakse maatriksi A reavektorite alamruumiks
ja tähistatakse
lineaarset katet nimetatakse maatriksi A reavektorite alamruumiks
ja tähistatakse
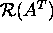 või
ran(AT).
või
ran(AT).
Definitsioon 2.4.3. Maatriksi astakuks nimetatakse suurimat naturaalarvu k, mille korral maatriksil leidub nullist erinev k-järku miinor. Maatriksi A astakut tähistatakse rank(A).
Olgu rank(A)=r. Maatriksi astaku kohta käiva teoreemi põhjal peab paika
Lause 2.4.1. Maatriksi
astak on võrdne tema reavektorite (veeruvektorite) alamruumi
mõõtmega, so
![]()
Definitsioon 2.4.4. Maatriksi
A (parempoolseks) nullruumiks nimetatakse võrrandisüsteemi
![]()
kõigi lahendite
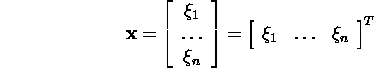
hulka. See on alamruum, mida
tähistatakse sümboliga ![]() või null(A).
või null(A).
Lause 2.4.2. Mistahes
maatriksi ![]() ,
mille astak on r, korral
,
mille astak on r, korral
![]()
Tõestus. Süsteemimaatriksi A
astakuks on r ja muutujate arvuks võrrandisüsteemis
(4) on n. Järelikult süsteemi vabadusastmete arvuks on
n-r. Vabadusastmete arv näitab nullruumi
mõõdet. Seega,
![]() Süsteem (4) on kirja pandav kujul
Süsteem (4) on kirja pandav kujul
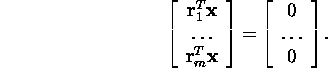
Seega ![]()
![]()
![]() =1:m),
st maatriksi A reavektorid on risti maatriksi A nullruumi
=1:m),
st maatriksi A reavektorid on risti maatriksi A nullruumi
![]() suvalise vektoriga ja seega
suvalise vektoriga ja seega ![]() Kuna lisaks
Kuna lisaks ![]() ja
ja ![]() siis
siis ![]() ja ruumi
ja ruumi ![]() esitub otsesummana
esitub otsesummana
![]()
Definitsioon 2.4.5. Maatriksi
A vasakpoolseks nullruumiks nimetatakse võrrandisüsteemi
![]()
kõigi lahendite

hulka ja tähistatakse ![]() või null(AT).
või null(AT).
Lause 2.4.3. Mistahes
maatriksi ![]() ,
mille astak on r, korral
,
mille astak on r, korral
![]()
Tõestus. Süsteemimaatriksi AT
astakuks on r ja muutujate arvuks võrrandisüsteemis
(5) on m. Järelikult on süsteemi vabadusastmete arvuks
m-r ja
![]()
Süsteem (5) on esitatav kujul
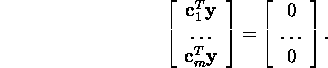
Seega
![]()
![]() =1:m)
ja
=1:m)
ja ![]() Kuna
Kuna ![]() ja
ja ![]() siis
siis ![]() ja ruumi Rm esitub otsesummana
ja ruumi Rm esitub otsesummana
![]()
Näide 2.4.1. Leiame maatriksi
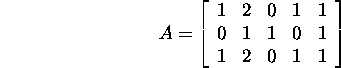
alamruumide ![]()
![]()
![]() ja
ja ![]() mõõtmed ja baasid.
Illustreerime lausete 2.4.2 ja 2.4.3
väiteid antud näite korral.
mõõtmed ja baasid.
Illustreerime lausete 2.4.2 ja 2.4.3
väiteid antud näite korral.
Alustame ruumi ![]() uurimisest, lahutades maatriksi A teisest veerust kahekordse esimese
veeru,
uurimisest, lahutades maatriksi A teisest veerust kahekordse esimese
veeru,
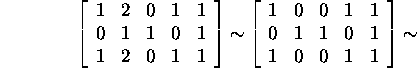
ja siis kolmandast veerust uue teise, neljandast veerust esimese ning viiendast
veerust esimese veeru ja uue teise
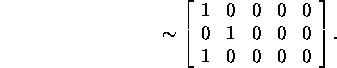
Siin sümbol "![]() "
maatriksite vahel tähistab seda, et on säilunud
"
maatriksite vahel tähistab seda, et on säilunud ![]() Viimasel maatriksil on nullist erinevaid veerge 2
Viimasel maatriksil on nullist erinevaid veerge 2 ![]()
![]() Baasiks ruumile
Baasiks ruumile ![]() saame
saame
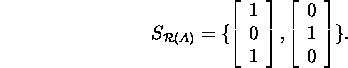
Ruumi ![]() kirjeldamiseks lahendame süsteemi (5) :
kirjeldamiseks lahendame süsteemi (5) :
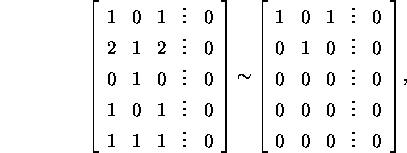
st
![]()
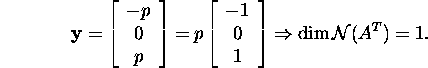
Seega ruumi ![]() baas on
baas on
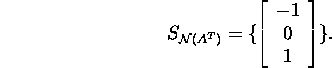
Kontrollime skalaarkorrutise
abil, et ![]()
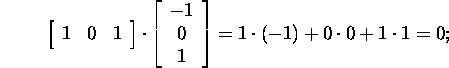
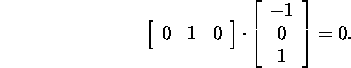
Ühend ![]() sisaldab kolme lineaarselt sõltumatut
sisaldab kolme lineaarselt sõltumatut
![]() vektorit ja on seega baasiks
ruumile
vektorit ja on seega baasiks
ruumile ![]() ning järelikult
ning järelikult ![]() Ruumi
Ruumi ![]() kirjeldamiseks leiame tema dimensiooni
ja baasi:
kirjeldamiseks leiame tema dimensiooni
ja baasi:
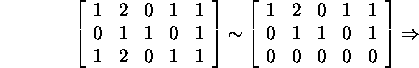
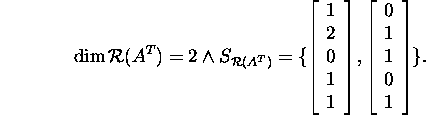
Ruumi ![]() kirjeldamiseks lahendame süsteemi (4):
kirjeldamiseks lahendame süsteemi (4):
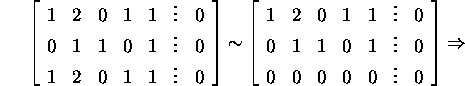
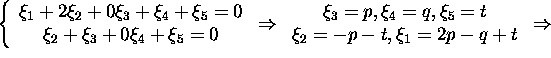
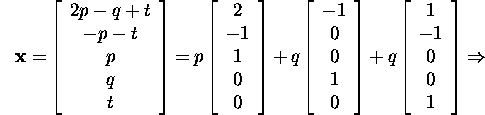
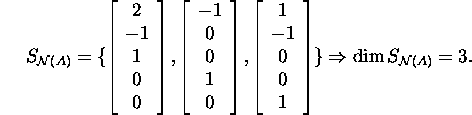
Baasi ![]() vektorid on risti baasi
vektorid on risti baasi ![]() vektoritega ja seega
vektoritega ja seega ![]() ning ühend
ning ühend ![]() moodustab baasi ruumile
moodustab baasi ruumile ![]() järelikult
järelikult
![]()
Ülesanne 2.4.1. Olgu ![]() Näidake, et
Näidake, et ![]()
Ülesanne 2.4.2. Näidake, et
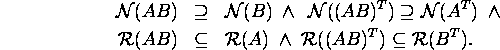
Ülesanne 2.4.3.* Leidke maatriksi
A alamruumide ![]()
![]()
![]() ja
ja ![]() mõõtmed ja baasid.
Illustreerige lausete 2.4.2 ja 2.4.3
väiteid maatriksi A korral, kui
mõõtmed ja baasid.
Illustreerige lausete 2.4.2 ja 2.4.3
väiteid maatriksi A korral, kui
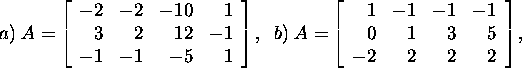
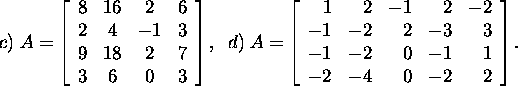
Ülesanne 2.4.4.* Leidke maatriksi
AB alamruumide ![]()
![]()
![]() ja
ja ![]() mõõtmed ja baasid,
kui
mõõtmed ja baasid,
kui
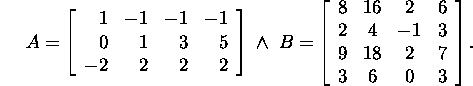
Võrrelge saadud tulemusi ülesande 2.4.3 alaülesannetes
b ja c saadud tulemustega.
Peatüki
algus: Maatriksid
Eelmine: Determinandid
Järgmine: Maatriksi
omaväärt used ja omavektorid