Peatüki algus: Maatriksid
Eelmine: Maatriksi neli alamruumi
Järgmine: Schuri lahutus

Definitsioon 2.5.1. Kui
 
kus A , ja on arv, siis arvu nimetatakse maatriksi A omaväärtuseks ja vektorit sellele omaväärtusele vastavaks maatriksi A (parempoolseks) omavektoriks.

Definitsioon 2.5.2. Vektorit nimetatakse maatriksi A vasakpoolseks omavektoriks, kui kus on transponeeritud kaasmaatriks.

Lause 2.5.1. Kui on omaväärtusele vastav maatriksi A vasakpoolne omavektor, siis see on omaväärtusele vastav maatriksi A^H parempoolne omavektor.

Tõestus. Saame väidete ahela

Nendime, et kui on omaväärtusele vastav omavektor, siis on seda ka kus . Seos (6) on esitatav kujul
 
kus I on ühikmaatriks. Kuna omaväärtusprobleemil (6) on iga ruutmaatriksi A korral omavektoriks nullvektor, siis järgnevas piirdume vaid mittetriviaalsete omavektorite uurimisega. Seos (7) kujutab endast homogeenset lineaarset algebralist võrrandisüsteemi, millel on mittetriviaalseid lahendeid vaid siis, kui selle süsteemi maatriks on singulaarne, st
 
Võrrandit (8) nimetatakse maatriksi A karakteristlikuks võrrandiks ja polünoomi

nimetatakse maatriksi A karakteristlikuks polünoomiks. Võrrand (8) on n-järku algebraline võrrand suuruse suhtes ning on kirja pandav kujul:
 
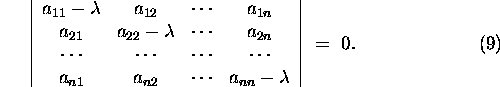
Algebra põhiteoreemi kohaselt on maatriksil parajasti n omaväärtust, arvestades kordsust.

Definitsioon 2.5.3. Maatriksi kõigi omaväärtuste hulka (siin võib olla võrdseid!) nimetatakse maatriksi A spektriks ja tähistatakse

Näide 2.5.1. Leida maatriksi

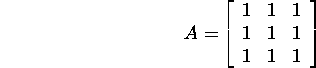
omaväärtused ja omavektorid.

Koostame antud maatriksile vastava karakteristliku võrrandi (9):

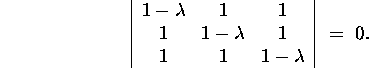
Arvutades determinandi, saame kuupvõrrandi

mille lahendeiks on ja Leiame omaväärtustele vastavad omavektorid. Selleks paigutame süsteemi (7) suuruse väärtuse 0 ja lahendame saadud süsteemi:

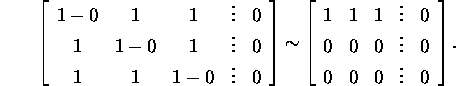
Sõltumatuid võrrandeid jääb üks,

ja süsteemi vabadusastmete arv on 2 ning süsteemi üldlahendiks on

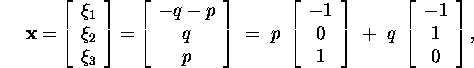
kus p ja q suvalised reaalarvud. Järelikult, omaväärtustele vastavad omavektorid moodustavad ruumi kahemõõtmelise alamruumi, mille baasivektoreiks võime valida vektorid ja vektorid Omaväärtusele vastavate omavektorite leidmiseks tuleb võrrandisüsteemis (7) suurus asendada selle väärtusega 3. Tulemusena tuleb lahendada võrrandisüsteem:



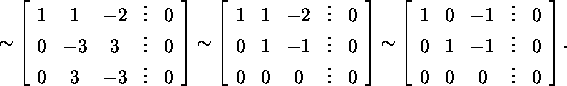
Selle süsteemi vabadusastmete arv on 1 ning maatriksi A omaväärtusele vastavad omavektorid avalduvad kujul

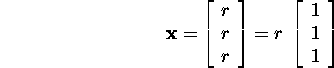
ja moodustavad ruumis ühemõõtmelise alamruumi, baasivektoriga

Ülesanne 2.5.1.^* Leidke maatriksi A omaväärtused ja omavektorid, kui

Ülesanne 2.5.2.^* Leidke maatriksi A omaväärtused ja omavektorid, kui

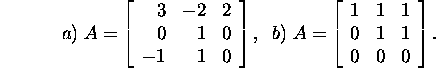
Lause 2.5.2. Kui on maatriksi A omaväärtused , siis

Tõestus. Karakteristliku võrrandi (8) vasak pool, nullkohtadega on esitatav kujul
 
Võttes selles seoses saame lause väite.

Järeldus. 2.5.1. Regulaarse maatriksi A ükski omaväärtused ei ole 0.

Lause 2.5.3. Kui on regulaarse maatriksi A omaväärtusele vastav omavektor, siis sama vektor on pöördmaatriks i A^-1 omaväärtusele vastav omavektor.

Tõestuseks korrutame seose (6) mõlemat poolt vasakult maatriksiga A^-1. Leiame, et ehk

Lause 2.5.4. Kui on maatriksi A omaväärtusele vastav omavektor, siis sama vektor on maatriksi A ² omaväärtusele vastavaks omavektoriks.

Tõestus. See väide järeldub võrduste ahelast:

Ülesanne 2.5.3.^* Olgu suurused maatriksi omaväärtused. Tõestage, et suurused on maatriksi omaväärtused.

Ülesanne 2.5.4.^* Tõestage, et kui suurused on maatriksi omaväärtused, siis suurused on maatriksi omaväärtused.

Lause 2.5.5. Maatriksi A jälg, st tema peadiagonaalil paiknevate elementide summa, võrdub maatriksi A kõigi omaväärtuste summaga.

Tõestuseks kasutame seost (10). Selle seose vasaku poole arenduses suuruse astmete järgi on astme kordajaks ja paremas pooles

Näide 2.5.2.^* Olgu teada maatriksi

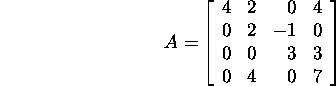
kolm omaväärtust: Leiame maatriksi A neljanda omaväärtuse ja determinandi.
Kuna maatriksi A jälg võrdub maatriksi A kõigi omaväärtuste summaga, siis

Leiame maatriksi A determinandi

Ülesanne 2.5.5.^* On teada, et maatriksi

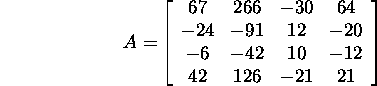
kolm omaväärtust: Leidke maatriksi A neljas omaväärtus ja determinant.

Lause 2.5.6. Nii ülemise kui ka alumise kolmnurkse maatriksi omaväärtusteks on kõik peadiagonaali elemendid ja ainult need.

Tõestus. Vaatleme selle väite tõestust ülemise kolmnurkse maatriksi A korral. Koostame vastava karakteristliku võrrandi

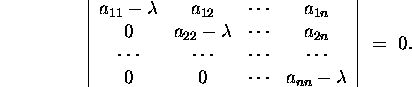
Determinandi arendamine annab karakteristlikule võrrandile kuju

Ülesanne 2.5.6.^* Leidke maatriksi A omaväärtused ja omavektorid, kui

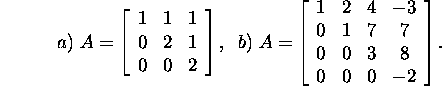
Lause 2.5.7. Maatriksi A erinevatele omaväärtustele vastavad omavektorid on lineaarselt sõltumatud.

Tõestus. Olgu maatriksi A erinevatele omaväärtustele vastavad omavektorid. Näitame, et nende omavektorite süsteem on lineaarselt sõltumatu. Lihtsuse mõttes viime selle tõestuse läbi vaid k=2 korral. Oletame väitevastaselt, et vektorite süsteem on lineaarselt sõltuv, st
 
Korrutame seoses (11) esineva võrduse mõlemat poolt vasakult maatriksiga A. Saame,
 
ehk
 
Korrutades seoses (11) esinevat võrdust suurusega ja lahutades saadud tulemuse seosest (13), saame

Selle seose vasakus pooles saab nulliga võrduda vaid esimene tegur, Analoogiliselt, korrutades seoses (11) esinevat võrdust suurusega jõuame võrduseni Seega mis on vastuolus eeldusega (11). Järelikult, omavektorite süsteem on lineaarselt sõltumatu.

Oletame, et maatriksi A omavektorite süsteem on lineaarselt sõltumatu. Moodustame ruutmaatriksi S, valides esimeseks veeruvektoriks vektori teiseks veeruvektoriks vektori n-ndaks veeruvektoriks vektori st
 
Tähistame
 
Eelpool toodud näite 2.5.1 korral

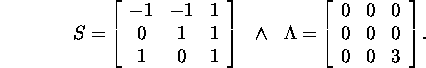
Lause 2.5.8. Kui maatriksil A on n lineaarselt sõltumatut omavektorit mis vastavad omaväärtustele siis maatriks A on esitatav kujul
 
kus maatriksid S ja on määratud vastavalt seostega (14) ja (15) .

Tõestuseks piisab näidata, et
 
Lähtume seose (17) vasakust poolest:

Lähtume seose (17) paremast poolest:



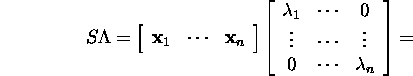
Järelikult peab seos (17) paika, ja seega ka seos (16), aga samuti ka seos
 

Näide 2.5.3.^* Leiame -maatriksi A, mille omaväärtusi ja neile vastavaid omavektoreid me teame:





Kuna otsitav maatriks A on esitatav kujul kus

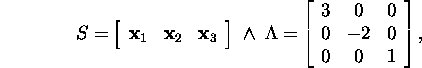
siis

:

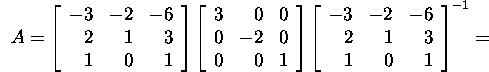
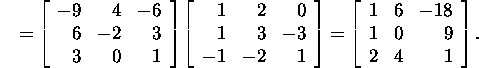
Ülesanne 2.5.7.^* Leiame -maatriksi A, mille omaväärtusi ja neile vastavaid omavektoreid me teame:

Ülesanne 2.5.8.^* Leiame -maatriksi A, mille omaväärtusi ja neile vastavaid omavektoreid me teame:

Näide 2.5.4.^* Leiame maatriksid A¹⁰⁰ ja A¹⁵⁵, kui

Kuna

ja

ning

siis



ja

Ülesanne 2.5.9.^* Leidke maatriksid A¹⁰⁰ ja A¹⁵⁵, kui

Lause 2.5.9. Kui maatriksi A ja B kõik omaväärtused on ühekordsed ning maatriksid A ja B on kommuteeruvad, siis neil on ühised omavektorid.

Tõestame selle väite. Olgu maatriksi A omaväärtusele vastav omavektor, st peab paika seos (6). Korrutame seose (6) mõlemat poolt vasakult maatriksiga B ja arvestame eeldust (maatriksite A ja B kommuteeruvust). Tulemuseks saame seoste ahela:



Seega, kui on maatriksi A omaväärtusele vastav omavektor, sii s ka on maatriksi samale omaväärtusele vastav omavektor. Kuna maatriksi A ühekordsele omaväärtusele vastav omavektorite hulk on ruumi ühemõõtmeline alamruum, siis vektorid ja on kollineaarsed, st

Järelikult, maatriksi A omaväärtusele vastav omavektor x on ka maatriksi B omavektoriks, mis vastab maatriksi B omaväärtusele . Analoogiliselt saab näidata, et maatriksi B iga omavektor on ka maatriksi A omavektor.

Lause 2.5.10. Kui maatriksitel A, B on n ühist lineaarselt sõltumatut omavektorit, siis need maatriksid on kommuteeruvad.

Tõestus. Lause 2.5.8 põhjal on need maatriksid esitatavad kujul
 
kus S on neist n omavektorist kui veeruvektorist moodustatud maatriks ja on diagonaalmaatriks, mille peadigonaalil on maatriksi A vastavad omaväärtused ning on diagonaalmaatriks, mille diagonaalil on maatriksi B vastavad omaväärtused. Leiame korrutised AB ja BA, kasutades seoses (19) antud esitusi:

ja

Kuna diagonaalmaatriksid ja on kommuteeruvad, siis AB=BA, mida oligi vaja tõestada.

Peatüki algus: Maatriksid
Eelmine: Maatriksi neli alamruumi
Järgmine: Schuri lahutus >