Eelmine: Vektori norm
Järgmine peatükk: Maatriksid
Ortogonaalsed vektorid
Definitsioon 1.6.1. Skalaarkorrutamisega vektorruumi X vektoreid x ja y nimetatakse ortogonaalseteks, kui
Peatüki
algus: Vektorid
Eelmine: Vektori
norm
Järgmine peatükk: Maatriksid
Ortogonaalsed
vektorid
Definitsioon 1.6.1.
Skalaarkorrutamisega
vektorruumi
X
vektoreid
x
ja
y
nimetatakse ortogonaalseteks, kui
![]() ja tähistatakse
ja tähistatakse
![]() Vektorruumi
X
vektorit
x
nimetatakse ortogonaalseks hulgaga
Vektorruumi
X
vektorit
x
nimetatakse ortogonaalseks hulgaga ![]() kui
kui ![]()
Ülesanne 1.6.1.* Leidke kõik
vektorid, mis on ortogonaalsed nii vektoriga
![]() kui ka vektoriga
kui ka vektoriga ![]()
Definitsioon 1.6.2. Öeldakse,
et vektorruumi
X
hulgad Y ja Z on ortogonaalsed, kui ![]()
Definitsioon 1.6.3. Jada
![]() skalaarkorrutamisega vektorruumi
X
nimetatakse Cauchy jadaks, kui vastavalt igale etteantud arvule
skalaarkorrutamisega vektorruumi
X
nimetatakse Cauchy jadaks, kui vastavalt igale etteantud arvule
![]() leidub naturaalarv n0 nii, et mistahes
leidub naturaalarv n0 nii, et mistahes ![]() ja n>n0 korral
ja n>n0 korral
![]()
Definitsioon 1.6.4. Skalaarkorrutamisega vektorruumi X nimetatakse täielikuks, kui temas iga Cauchy jada on koonduv selle ruumi X punktiks.
Definitsioon 1.6.5.
Hilberti ruumiks ![]() nimetatakse kompleksset skalaarkorrutamisega
vektorruumi, mis osutub normi
nimetatakse kompleksset skalaarkorrutamisega
vektorruumi, mis osutub normi ![]() järgi koondumise mõttes täielikuks.
järgi koondumise mõttes täielikuks.
Lause 1.6.1. Ruum ![]() skalaarkorrutamisega
skalaarkorrutamisega ![]() on
Hilberti ruum.
on
Hilberti ruum.
Lause 1.6.2. Lõigul ![]() integreeruva ruuduga funktsioonide ruum
integreeruva ruuduga funktsioonide ruum ![]() skalaarkorrutisega
skalaarkorrutisega ![]() on Hilberti ruum.
on Hilberti ruum.
Lause 1.6.3. Skalaarkorrutamisega vektorruumi X vektorite ortogonaalsusel on järgmised omadused (1-4):
Tõestame need väited:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Definitsioon 1.6.6. Hulga
![]() ortogonaalseks täiendiks nimetatakse hulka
ortogonaalseks täiendiks nimetatakse hulka ![]() ruumi
X
kõigist vektoritest, mis on ortogonaalsed
hulgaga Y, st
ruumi
X
kõigist vektoritest, mis on ortogonaalsed
hulgaga Y, st
![]()
Ülesanne 1.6.2.* Olgu ![]() Leidke hulga U ortogonaalne täiend.
Leidke hulga U ortogonaalne täiend.
Lause 1.6.4. Kui
X
on skalaarkorrutamisega vektorruum,
![]()
![]() ja
ja ![]() siis
siis ![]() Kui lisaks
X
on täielik, st on Hilberti
ruum, siis
Kui lisaks
X
on täielik, st on Hilberti
ruum, siis ![]()
Tõestus. Lause 1.6.3
väidete 3 ja 4 põhjal ![]() .
Kui
.
Kui ![]() st
st 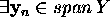 , selline, et
, selline, et ![]() siis arvestades ortogonaalsust
siis arvestades ortogonaalsust ![]() ja lause 1.6.3 väidet 5, saame
ja lause 1.6.3 väidet 5, saame ![]() , st
, st ![]()
Lause 1.6.5. Hulga ![]() ortogonaalne täiend
ortogonaalne täiend ![]() on ruumi
X
alamruum. Hulga
on ruumi
X
alamruum. Hulga ![]() ortogonaalne täiend
ortogonaalne täiend ![]() on Hilberti ruumi
on Hilberti ruumi ![]() kinnine alamruum, st
kinnine alamruum, st ![]() on ruumi
on ruumi ![]() alamruum, mis sisaldab kõik oma rajapunktid.
alamruum, mis sisaldab kõik oma rajapunktid.
Tõestus. Lause
1.2.1 põhjal on piisav lause 1.6.5 esimese väite tõestamiseks
näidata, et ![]() on kinnine vektorite liitmise ja skalaariga korrutamise suhtes. See järeldub
lause 1.6.3 väidetest 3 ja 4. Sama lause
väite 5 põhjal kehtib ka lause 1.6.5 teine väide.
on kinnine vektorite liitmise ja skalaariga korrutamise suhtes. See järeldub
lause 1.6.3 väidetest 3 ja 4. Sama lause
väite 5 põhjal kehtib ka lause 1.6.5 teine väide.
Lause 1.6.6. Kui Y on Hilberti
ruumi ![]() kinnine alamruum, siis iga
kinnine alamruum, siis iga ![]() esitub ühesel viisil summana
esitub ühesel viisil summana ![]()
![]()
Järeldus 1.6.1. Kui ![]() on Hilberti ruumi
on Hilberti ruumi ![]() kinnine alamruum, siis ruum
kinnine alamruum, siis ruum ![]() avaldub kinniste alamruumide
avaldub kinniste alamruumide ![]() ja
ja ![]() otsesummana
otsesummana ![]() ning
ning ![]()
Definitsioon 1.6.7.
Hilberti ruumi ![]() vektori
x
kaugus alamruumist
vektori
x
kaugus alamruumist ![]() defineeritakse valemiga
defineeritakse valemiga
![]()
Lause 1.6.7. Kui ![]() on Hilberti ruumi
on Hilberti ruumi ![]() kinnine alamruum ja
kinnine alamruum ja ![]() ,
siis leidub selline üheselt määratud
,
siis leidub selline üheselt määratud ![]() et
et ![]()
Definitsioon 1.6.8.
y
nimetatakse vektori
x
ristprojektsiooniks alamruumile ![]()
Definitsioon
1.6.9.Vektorite süsteemi ![]() nimetatakse ortogonaalseks, kui
nimetatakse ortogonaalseks, kui ![]() ,
kus
,
kus ![]() on Kroneckeri sümbol. Vektorite süsteemi
on Kroneckeri sümbol. Vektorite süsteemi
![]() nimetatakse ortonormeerituks, kui
nimetatakse ortonormeerituks, kui ![]() .
.
Näide 1.6.1. Vektorite süsteem ![]() (k=1:n),
kus
(k=1:n),
kus
![]()
on ruumis ![]() ortonormeeritud.
ortonormeeritud.
Näide 1.6.2. Vektorite süsteem
![]()
on ortonormeeritud süsteem ruumis ![]()
Näide 1.6.3. Vektorite süsteem ![]() on ortonormeeritud süsteem ruumis
on ortonormeeritud süsteem ruumis ![]() Tõesti,
Tõesti,
![]()
![]()
Lause 1.6.8. (Gram-Schmidti
ortogonaliseerimisteoreem). Olgu ![]() lineaarselt sõltumatu vektorite
süsteem skalaarkorrutamisega
vektorruumis
lineaarselt sõltumatu vektorite
süsteem skalaarkorrutamisega
vektorruumis ![]() .
Siis leidub selline ortonormeeritud süsteem
.
Siis leidub selline ortonormeeritud süsteem
![]() et
et
![]()
Tõestame selle väite matemaatilise
induktsiooni meetodil. Juhul k=1 defineerime ![]() ja tõesti,
ja tõesti, ![]() Induktsiooni-baas on olemas. Näitame induktsiooni-sammu lubatavust.
Eeldame, et lause väide peab paika k=i-1 korral, st
leidub selline ortonormeeritud süsteem
Induktsiooni-baas on olemas. Näitame induktsiooni-sammu lubatavust.
Eeldame, et lause väide peab paika k=i-1 korral, st
leidub selline ortonormeeritud süsteem
![]() et
et ![]() Vaatleme vektorit
Vaatleme vektorit
![]()
Kordajad ![]() valime nii, et
valime nii, et ![]() ,
st
,
st ![]() Saame i-1 tingimust:
Saame i-1 tingimust:
![]() ehk
ehk ![]() .
Seega,
.
Seega,
![]()
Valime ![]() Kuna
Kuna
![]()
siis vektorite ![]() ja
ja ![]() konstruktsiooni põhjal
konstruktsiooni põhjal ![]() Seega
Seega
![]()
Vektori ![]() esitusest järeldub, et
esitusest järeldub, et ![]() on vektorite
on vektorite ![]() lineaarne kombinatsioon. Järelikult,
lineaarne kombinatsioon. Järelikult,
![]()
Seega
![]()
Näide 1.6.4. On antud ruumi ![]() vektorite süsteem
vektorite süsteem
![]() kus
kus
![]()
Leiame sellise ortonormeeritud süsteemi
![]() ,
et
,
et
![]()
Lause 1.6.8 tõestuses esitatud ortogonaliseerimisprotsessi rakendamiseks,
esiteks, kontrollime, kas süsteem ![]() on lineaarselt sõltumatu
(võib ka mitte kontrollida, see selgub ka ortogonaliseerimise käigus):
on lineaarselt sõltumatu
(võib ka mitte kontrollida, see selgub ka ortogonaliseerimise käigus):
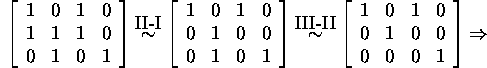
![]() on lineaarselt sõltumatu. Leiame vektori
on lineaarselt sõltumatu. Leiame vektori
![]()
Vektor ![]() avaldub kujul:
avaldub kujul:
![]()
Kuna ![]() siis
siis ![]() Vektor
Vektor ![]() avaldub kujul:
avaldub kujul:
![]()
![]()
Seega,
![]()
Näide 1.6.5. On antud ruumi ![]() lineaarselt sõltumatu vektorite
süsteem
lineaarselt sõltumatu vektorite
süsteem ![]() kus
kus ![]()
![]() ja
ja ![]() Leiame sellise ortonormeeritud süsteemi
Leiame sellise ortonormeeritud süsteemi
![]() ,
et
,
et
![]()
Veenduda, et süsteem ![]() on lineaarselt sõltumatu. Leiame vektori
on lineaarselt sõltumatu. Leiame vektori
![]()
Vektor ![]() avaldub kujul:
avaldub kujul:
![]()
Seega,
![]()
Vektor ![]() avaldub kujul:
avaldub kujul:
![]()
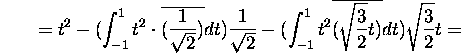
![]()
Järelikult,
![]()
![]()
Funktsioonid ![]() ja
ja ![]() on normeeritud Legendre'i polünoomid lõigul
on normeeritud Legendre'i polünoomid lõigul ![]()
Ülesanne 1.6.1. Näidake, et paarikaupa
ortogonaalsete vektorite süsteem ![]() on lineaarselt sõltumatu.
Peatüki
algus: Vektorid
on lineaarselt sõltumatu.
Peatüki
algus: Vektorid
Eelmine: Vektori
norm
Järgmine peatükk: Maatriksid