Peatüki algus: Vektorid
Eelmine: Vektorruumid
Järgmine: Vektorite lineaarne sõltuvus.

Definitsioon 1.2.1. Vektorruumi (üle korpuse ) vektorite hulka , mis on vektorruum ruumis defineeritud vektorite liitmise ja vektori arvuga korrutamise suhtes, nimetatakse vektorruumi alamruumiks ning kirjutatakse

Lause1.2.1Vektorruumi vektorite hulk on vektorruumi alamruum parajasti siis, kui iga kahe vektori ja iga arvu korral ka vektorid ja kuuluvad hulka .

Tõestus. Tarvilikkus on ilmne. Piisavuse tõestamiseks tuleb näidata, et nende tingimuste korral on täidetud vektorruumi tingimused 1-8. Kontrollime tingimuse 1 täidetust. Olgu Eelduse kohaselt . Kuna on vektorruum, siis jaoks on rahuldatud aksioom 1 ja seega . Järelikult, korral on aksioom 1 samuti rahuldatud. Põhjendame veel tingimuse 4 täidetuse. Olgu Eelduse põhjal Teisalt, ruumis kehtib lause 1 põhjal seos Seega, koos vektoriga x kuulub hulka ka tema vastandvektor , st tingimus 4 on täidetud. Tõestada iseseisvalt tingimuste 2, 3 ja 5-8 täidetus.

Näide 1.2.1. Kõigi lõigul pidevate funktsioonide vektorruum üle on näites 1.1.3 toodud vektorruumi alamruum. Kuna kahe lõigul pideva funktsiooni summa on sel lõigul pidev funktsioon ja lõigul pideva funktsiooni korrutis arvuga on sel lõigul pidev funktsioon, siis lause 1.2.1 põhjal on vektorruumi alamruum.

Näide 1.2.2. Olgu kõigi reaalsete kordajatega ülimalt n-astme polünoomide hulk. Defineerime kahe polünoomi liitmise ja polünoomi reaalarvuga korrutamise tavapärasel viisil. Tulemuseks saame ülimalt n-astme polünoomide vektorruumi Kui sümboliga tähistada lõigul määratud ülimalt n-astme polünoomide vektorruumi, siis on vektorruumi alamruum.

Lause 1.2.2. Kui on vektorruumi alamruumid, siis nende alamruumide ühisosa on samuti vektorruumi alamruum.

Tõestage!

Näide 1.2.3.^* Näitame, et hulk

on alamruum maatriksite vektorruumis
Hulk on kinnine liitmise ja skalaariga korrutamise suhtes, sest

ja

Seetõttu hulk on alamruum maatriksite vektorruumis

Ülesanne 1.2.1.^* Tõestage, et kõigi sümmeetriliste maatriksite hulk moodustab alamruumi ruutmaatriksite vektorruumis

Lause 1.2.3. Kui on ruumi alamruumid ja

on nende alamruumide summa, siis on alamruum ruumis

Definitsioon 1.2.2. Kui iga on ühesel viisil esitatav kujul

siis öeldakse, et on alamruumide otsesumma ja tähistatakse

Definitsioon 1.2.3. Vektorruumi (üle korpuse elementide lineaarseks kombinatsiooniks nimetatakse ruumi iga elementi, mida saab esitada kujul kus

Definitsioon 1.2.4. Hulga lineaarseks katteks nimetatakse hulga Z kõikvõimalike lineaarsete kombinatsioonide hulka Hulga lineaarset katet tähistatakse sümboliga

Näide 1.2.3. Olgu ja Siis
Tõestage!

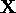Lause1.2.4. Hulga Z lineaarne kate on vektorruumi vähim alamruum, mis sisaldab hulka

Tõestus. Tõestame esiteks, et on ruumi alamruum. Lause 1.2.1 põhjal on selleks piisav näidata, et on kinnine vektorite liitmise ja vektori arvuga korrutamise suhtes:







Seega on ruumi alamruum. Näitame, et on vähim hulka Z sisaldav ruumi alamruum. Olgu ruumi mingi alamruum, mille korral Näitame, et Kuna ja on alamruum, siis hulga Z elementide suvaline lineaarkombinatsioon kuulub alamruumi Järelikult kuulub ruumi ka kui kõigi selliste lineaarkombinatsioonide hulk.

Järeldus 1.2.1. Vektorruumi alamhulk on alamruum parajasti siis, kui ta ühtib oma lineaarse kattega, so

Ülesanne 1.2.2.^* Kas vektor kuulub alamruumi kui