If n=1, then the Jordan block coincides with the given matrix and formula (9) is true. Let us suppose that the Jordan form of the matrix A is found by applying the Jordan block construction formula (9) if the order of the matrix A is smaller than n. we will use mathematical induction.
I step. Assuming that A is singular, ![]() Considering the corresponding
Considering the corresponding ![]() matrix we find that in this case the construction based on formulas
(9) is realizable. Namely, in the space
matrix we find that in this case the construction based on formulas
(9) is realizable. Namely, in the space ![]() there are r independent
vectors
there are r independent
vectors ![]() such that the following relations take place
such that the following relations take place
![]()
II step. Let us suppose that ![]() Every vector of the null space
Every vector of the null space
![]() is an eigenvector of the matrix A corresponding to the eigenvalue
of the matrix A
is an eigenvector of the matrix A corresponding to the eigenvalue
of the matrix A ![]() Therefore, there must be p chains on the I step which begin with
the eigenvectors corresponding
to the eigenvalue 0. We are
interested in the last vector of each such chain. Since the vectors
Therefore, there must be p chains on the I step which begin with
the eigenvectors corresponding
to the eigenvalue 0. We are
interested in the last vector of each such chain. Since the vectors ![]() belonging to the subspace
belonging to the subspace ![]() must also belong to the space
must also belong to the space ![]() then they have to be the linear combinations of the column vectors of the
matrix A
then they have to be the linear combinations of the column vectors of the
matrix A
![]()
with some ![]() .
Therefore, the vector
.
Therefore, the vector ![]() follows the vector
follows the vector ![]() in the chain corresponding to the eigenvalue
in the chain corresponding to the eigenvalue
![]() .
.
III step. Since ![]() there must be n-r-p more linearly
independent vectors
there must be n-r-p more linearly
independent vectors ![]() of the space
of the space ![]() in the orthogonal complement of the subspace
in the orthogonal complement of the subspace ![]() .
.
Proposition 5.3.1.
The algorithm of Filipov defines r vectors ![]() p vectors
p vectors ![]() and n-r-p vectors
and n-r-p vectors ![]() which determine the Jordan chains. These
vectors are linearly
independent and suit to be the column-vectors of the matrix X,
and J=X-1AX.
which determine the Jordan chains. These
vectors are linearly
independent and suit to be the column-vectors of the matrix X,
and J=X-1AX.
Proof. Look Strang
(1988, p. 457). ![]()
Example 5.3.1. Let us find the Jordan
normal form of the matrix
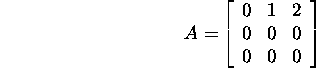
using the algorithm of Filipov.
I step. It comes out from the form of the matrix
that ![]() and
and ![]() Hence r=1 and there is a vector
Hence r=1 and there is a vector ![]() from this subspace
from this subspace ![]() satisfying the condition (10).
satisfying the condition (10).
II step. Let us find the basis
of the null space ![]() of the matrix A:
of the matrix A:
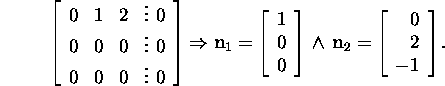
The vector ![]() belongs to the subspace
belongs to the subspace ![]() and
and ![]() We solve the system
We solve the system
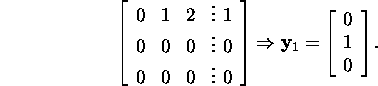
III step. We take for the vector ![]() the vector
the vector ![]() and form the matrix X:
and form the matrix X:
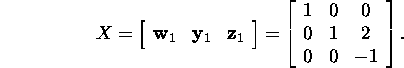
Now we find the inverse matrix
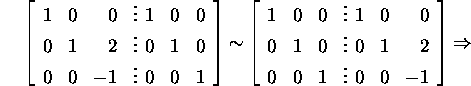
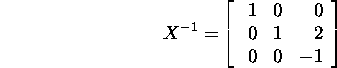
and the Jordan matrix
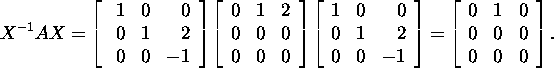
The software package ``Maple'' gives for the Jordan
decomposition:
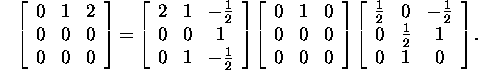
Since the matrix X in the Jordan decomposition of the matrix A is not uniquely defined, then for many problems it is of interest to choose the matrix X so that the conditional number k(X) were the least. Such a problem arose also in example 1.2.9.4.
Problem 5.3.1. Find the
Jordan decomposition of the matrix
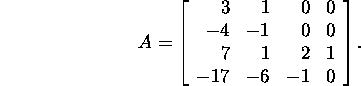
Problem 5.3.2.* Find the Jordan
decomposition of the matrix
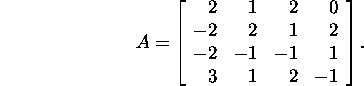
Problem 5.3.3.* Find the
Jordan decomposition of the matrix
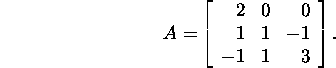
Problem 5.3.4. Let the Jordan
decomposition of the matrix ![]() be A=MJM-1. Show that
be A=MJM-1. Show that ![]()