Eigenvalues and Eigenvectors of a Matrix

Definition 2.5.1. If
 
where , and is a number, then the number is called an eigenvalue of the matrix A and the vector a (right) eigenvector of the matrix A corresponding to the eigenvalue .

Definition 2.5.2. The vector is called a (left) eigenvector of the matrix A if where is the transposed scew-matrix.

Proposition 2.5.1. If is a left eigenvector of the matrix A corresponding to the eigenvalue , then this is a right eigenvector corresponding to the eigenvalue .

Proof. We get a chain of assertions:

It is obvious that if is a eigenvector corresponding to the eigenvalue , then is an eigenvector, too. The equation (6) can be expressed in form
 
where I is the identity matrix of order n. As the null vector is an eigenvector for every square matrix A in eigenvalues problem (6), in following we will confine ourselves to the non-trivial eigenvectors. The equation (7) presents a system of homogeous linear algebraic equations that has a non-trivial solution if the matrix of the system is singular, i.e.,
 
The equation (8) is called the characteristic equation of the matrix A, and the polynomial

is called the characteristic polynomial of the matrix A. The equation (8) is an algebraic equation of order n with respect to , and it can be written down in form:
 
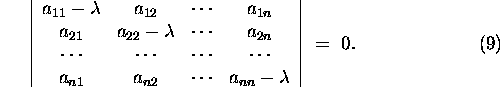
According to the fundamental theorem of algebra, the matrix has exactly n eigenvalues, taking into account their multiplicity.

Definition 2.5.3. The set of all eigenvalues of the matrix is called the spectre of the matrix A and denoted by

Example 2.5.1. Find the eigenvalues and eigenvectors of the matrix

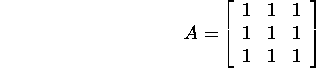
We compose the characteristic equation (9) corresponding to the given matrix:

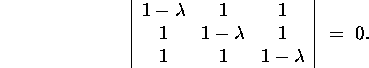
Calculating the determinant, we get the cubic equation

with the solutions and Let us find the eigenvectors corresponding to the eigenvalues . We replace in system (7) the variable by 0 and solve the equation:

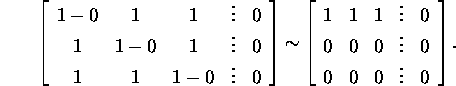
There is only one independent equation remained:

The number of degrees of freedom of the system is 2, and the general solution of the system is

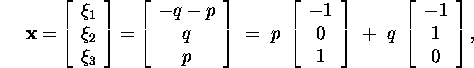
where p and q are arbitrary real numbers. Thus, the vectors that correspond to the eigenvalues form a two-dimensional subspace in the space , and vectors and can be chosen for its basis. To find the eigenvector corresponding to the eigenvalue we have to replace in the system of equations (7) the variable by 3. As a result, we get the system of equations:



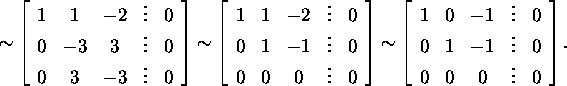
The number of degrees of freedom of this system is 1, and the eigenvectors of the matrix A corresponding to the eigenvalue can be expressed in form

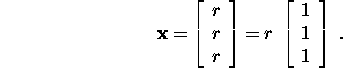
They form a one-dimensional subspace in with the basis vector

Problem 2.5.1.^* Find the eigenvalues and eigenvectors of the matrix A, where

Problem 2.5.2.^* Find the eigenvalues and eigenvectors of the matrix A, when

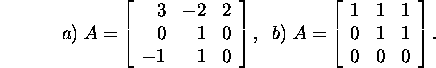
Proposition 2.5.2. If are the eigenvalues of the matrix A, then

Proof. The left side of the characteristic equation (8) with the zeros can be expressed in form
 
If we take in this equation we get the assertion of the proposition.

Corollary 2.5.1. Not a single one of the eigenvalues of a regular matrix A is equal to 0.

Proposition 2.5.3. If is an eigenvector of the regular matrix A corresponding to the eigenvalue , then the same vector is as eigenvector of the inverse matrix A^-1 corresponding to the eigenvalue .

To prove the assertion we multiply the both sides of the equality (6) on the left by the matrix A^-1. We get or

Proposition 2.5.4. If is an eigenvector of the matrix A corresponding to the eigenvalue , then the same vector is an eigenvector of the matrix A² corresponding to the eigenvalue .

Proof. This assertion follows from the chain:

Problem 2.5.3.^* Let be the eigenvalues of the matrix Prove that are the eigenvalues of the matrix .

Problem 2.5.4.^* Prove that if are the eigenvalues of the matrix , then are the eigenvalues of the matrix .

Proposition 2.5.5. The trace of the matrix A, i.e., the sum of the elements on the main diagonal, is equal to the sum of all eigenvalues of the matrix A.

To prove the assertion we will use the equality (10). In the expansion of the left side by the powers of the variable the coefficient by the power is and at the right side it is

Example 2.5.2.^* Let be known three eigenvalues and of the matrix

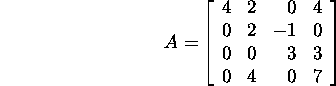
Let us find the forth eigenvalue of the matrix A and its determinant. Since the trace of the matrix A equals the sum af all eigenvalues,

Computing the determinant, we get

Problem 2.5.5.^* Let be known three eigenvalues and of the matrix

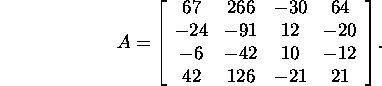
Find the forth eigenvalue of the matrix A and its determinant.

Proposition 2.5.6. The eigenvalues of both an upper triangular or a lower triangular matrix are the elements of the main diagonal, and only they.

Proof. Let us consider the case of an upper triangular matrix A. We form the characteristic equation

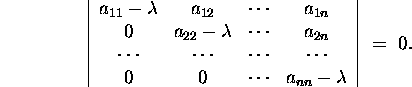
Expanding the determinant we get from here

Problem 2.5.6.^* Find eigenvalues and eigenvectors of the matrix A, where

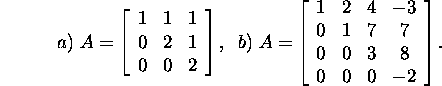
Proposition 2.5.7. The eigenvectors of the matrix A corresponding to the different eigenvalues are linearly independent.

Proof. Let be the eigenvectors of the matrix A corresponding to the different eigenvalues k= 2 : n). We will show that the system of these eigenvectors is linearly independent. Avoiding complicity we shall go through the proof in case k=2. Let us suppose that the antithesis is valid, i.e., the vector system is linearly independent:
 
Multiplying the equality in (11) on the left by matrix A, we get
 
or
 
Multiplying the equality in (11) by , and substracting the result from (13), we get

On the left in this equality only the first factor can equal 0. Analogously, multiplying in (11) by (11) by we get the equality . So and this is in contradiction with the assumption (11). Therefore, the system of eigenvectors is linearly independent.

Let us suppose that the system of eigenvectors of the matrix A is linearly independent. Let us form the matrix S, choosing the vector as the first column-vector, the vector as the second column-vector, the vector as the n-th column-vector, i.e.,
 
Let us denote
 
For the above example 2.5.1, we get

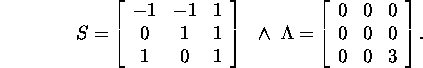
Proposition 2.5.8. If the matrix A has n linearly independent eigenvectors corresponding to the eigenvalues then the matrix A can be expressed in form
 
where the matrices S and are defined by (14) and (15).

For the proof it will suffer to show that
 
Let us start from the left side of (17):

From the right side of (17) we get:



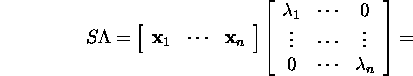
Therefore, equality (17) holds, and consequently equality (16), and also the equality
 

Example 2.5.3.^* Find a -matrix A which eigenvalues and corresponding eigenvectors are:





As the wanted matrix A can be represented in form where

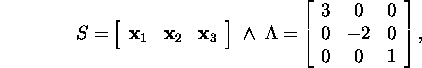
then

:

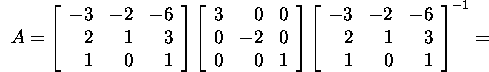
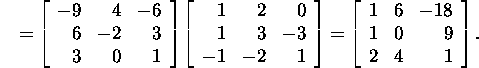
Problem 2.5.7.^* Find a -matrix A which eigenvalues and corresponding eigenvectors are:

Problem 2.5.8.^* Find a -matrix A which eigenvalues and corresponding eigenvectors are:

Example 2.5.4.^* Find matrices A¹⁰⁰ and A¹⁵⁵, where

Since



and

then



and

Problem 2.5.9.^* Find matrices A¹⁰⁰ and A¹⁵⁵, where

Proposition 2.5.9. If all the eigenvalues of the matrices A and B are single and the matrices A and B are commutative, then they have common eigenvectors.

Proof. Let be an eigenvector of the matrix A corresponding to the eigenvalue , i.e., it holds (6). Let us multiply both sides (6) on the left by the matrix B. Due to the commutability of the matrices A and B, we get the chain:

Thus, if is an eigenvector of the matrix A corresponding to the eigenvalue , then is also an eigenvector of the matrix A corresponding to the single eigenvalue is a one-dimensional subspace in , then the vectors and are collinear, i.e.,

Thus, the eigenvector of the matrix A corresponding to the eigenvalue is also the eigenvector of the matrix B corresponding to the eigenvalue Analogously one can show that each eigenvector of the matrix B is an eigenvector of the matrix A

Proposition 2.5.10. If the matrices A, B have n common linearly independent eigenvectors, then these matrices are commutative.

Proof. Due to proposition 2.5.8, these matrices can be expressed in form
 
where S is the matrix formed of the eigenvectors as column-vectors, and is a diagonal matrix with eigenvalues of the matrix A on the main diagonal, and is a diagonal matrix with the eigenvalues of the matrix B on the main diagonal. Let us find the products AB and BA, using the representation in (19):

and

As the diagonal matrices and are commutative, AB=BA, q.e.d.