It is not sufficient to find the eigenvalues of the matrix to obtain the Jordan form of this matrix.
Example 5.2.1. Let us find the Jordan
matrices J of the matrices
It is easy to find out that the spectres of 
and I are the same, 
Let us find the eigenvectors corresponding
to 
:
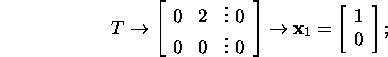
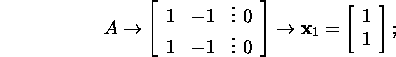
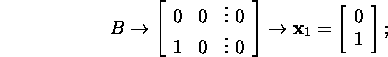
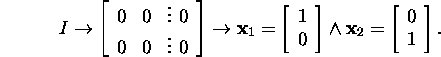
We see that the matrices 
and 
have only one independent eigenvector
and only one Jordan
block corresponding to the eigenvalue
,
and thus the matrices
and
have the same Jordan
matrix
The matrix I has two linearly
independent eigenvectors and,
consequently, two Jordan
blocks, and the corresponding Jordan
matrix coincides with the matrix I.
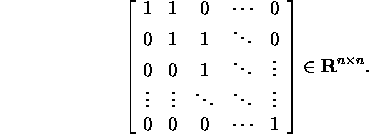
Problem 5.2.1. Verify that the matrix
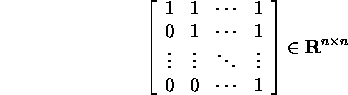
it corresponds the one-block Jordan
matrix
Example 5.2.2. Let us consider the Jordan
matrix
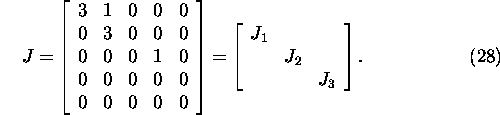
Let us find the eigenvectors corresponding
to the eigenvalue 
of multiplicity 2:
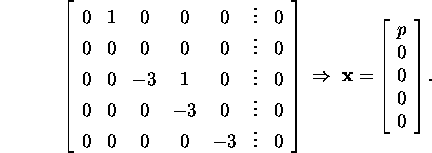
Therefore, to the eigenvalue
it corresponds one linearly
independent eigenvector
and one Jordan block
Let us find the eigenvectors
corresponding to the eigenvalue
of multiplicity 3:
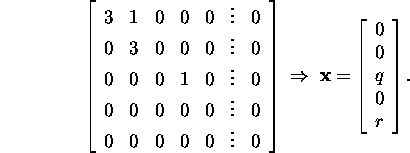
Hence to the eigenvalue
it corresponds two linearly
independent eigenvectors
and 
and two Jordan blocks
and
The question arises, what conditions mest setisfy the 
matrix A to have for the corresponding Jordan
matrix the J given by (5)? How to find the regular matrix X
such that
The first condition is 
but it is not sufficient. The eigenvalues
of the matrix A must be also considered. We express the relation
(6) in the form AX=XJ or
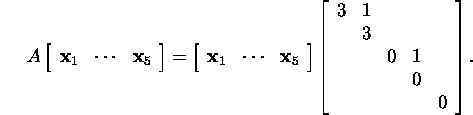
Having multiplied the matrices, we get the formulas
and
From the formulas (7)
and (8) it follows that similarly to the matrix J
the matrix A must have three eigenvectors
and 
In addition, the matrix A must have two generalized eigenvectors
or two first order flag vectors 
and 
It is said that the vector
belongs to the chain that begins with the vector 
and is defined by the formula (7). This chain determines
the Jordan block J1.
Two first formula of (8) define the second chain consisting
of the vectors 
and 
,
and this chain, in its turn, defines the Jordan
block J2. The last of the formulas (8)
defines the third chain consisting of the vector 
,
and this chain, in its turn, defines the Jordan
block J3.
Proposition 5.2.1.
The fixation of the Jordan
form of the matrix 
reduces to the finding of chains. Every chain starts
on the eigenvector of the
matrix A and for every value of the index i=1:n
The vectors 
are the column vectors of the matrix X, and every chain determines
one Jordan block.