The eigenvector ![]() of the matrix
of the matrix ![]() determines in the space
determines in the space ![]() a one-dimensional subspace that is invariant
with respect to the multiplication by the matrix A on the left.
a one-dimensional subspace that is invariant
with respect to the multiplication by the matrix A on the left.
Definition 2.6.1. The
subspace ![]() is called invariant with respect to the multiplication by the matrix A
on the left if
is called invariant with respect to the multiplication by the matrix A
on the left if ![]()
Proposition 2.6.1.
If ![]() and AX=XB, then the space
and AX=XB, then the space ![]() of the matrix X is invariant with respect
to the multiplication by the matrix A on the left and the space
of the matrix X is invariant with respect
to the multiplication by the matrix A on the left and the space
![]() is invariant with respect to the multiplication by the matrix B
on the right. In addition, the following connections
is invariant with respect to the multiplication by the matrix B
on the right. In addition, the following connections
![]()
and
![]()
holds.
Proof. If ![]() then
then
![]()
and
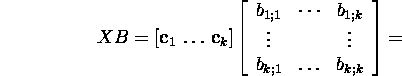
![]()
and
![]()
Therefore, the space ![]() of the column-vectors of the matrix X is invariant
with respect to the multiplication by the matrix A on the left.
Analogously, one can prove that the space
of the column-vectors of the matrix X is invariant
with respect to the multiplication by the matrix A on the left.
Analogously, one can prove that the space ![]() of the row-vectors is invariant with respect
to the multiplication by the matrix B on the right. If
of the row-vectors is invariant with respect
to the multiplication by the matrix B on the right. If ![]() then
then
![]()
i.e., ![]() is an eigenvalue of the matrix A
if
is an eigenvalue of the matrix A
if ![]() is the eigenvalue of the matrix B.
Naturally,
is the eigenvalue of the matrix B.
Naturally,
![]()
therefore, if the column-vectors of the matrix X are linearly
independent, then ![]() If
If ![]() and X is a regular square matrix
and X is a regular square matrix ![]() ,
then it follows from the equality AX=XB that A=XBX-1
and
,
then it follows from the equality AX=XB that A=XBX-1
and
![]()
i.e., every eigenvalue of the matrix
A is an eigenvalue of the matrix
B, ![]() ,
and thus
,
and thus ![]()
Definition 2.6.2. Matrices
![]() are said to be similar if there exists a regular matrix
are said to be similar if there exists a regular matrix ![]() such that A=XBX-1.
such that A=XBX-1.
Due to proposition 2.6.1
(the last assertion), the spectres of
two similar matrices are equal. We can get this result also directly:
![]()
![]()
Problem 2.6.1.* Are the matrices A
and B similar if
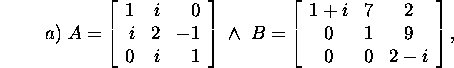
Proposition 2.6.2.
If ![]() and
and
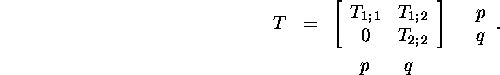
then ![]()
Proof. If ![]() i.e.,
i.e., ![]()
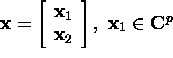 and
and ![]() then
then
![]()
If ![]() then
then
![]()
If ![]() then
then
![]()
Thus,
![]()
Since the potencies of the sets ![]() and
and ![]() are equal, then the proposition holds.
are equal, then the proposition holds. ![]()
Example 2.6.1. Using proposition
2.6.2, let us find the spectre of
the matrix
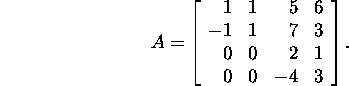
First, we find the eigenvalues of
the matrices 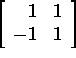 and
and 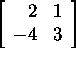 :
:
![]()
![]()
Thus, the spectre of the matrix is ![]()
Problem 2.6.2.* Find by the use
of proposition 2.6.2 the spectre
of the matrix A if
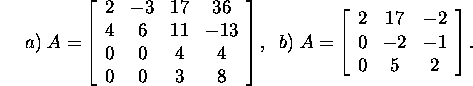
Definition 2.6.3. A
matrix ![]() is called a unitary matrix if QHQ=QQH=I.
is called a unitary matrix if QHQ=QQH=I.
Problem 2.6.3.* Is the matrix
Q a unitary matrix if
![]()
![]()
Proposition
2.6.3 (the QR factorisation theorem) . If ![]() ,
then the matrix A can be expressed in form A=QR, where
matrix
,
then the matrix A can be expressed in form A=QR, where
matrix ![]() is unitary matrix and matrix
is unitary matrix and matrix ![]() is an upper triangular matrix.
is an upper triangular matrix.
Proposition 2.6.4.
If ![]()
![]()
and rank(X)=p, then there exists a unitary
matrix ![]() such that
such that
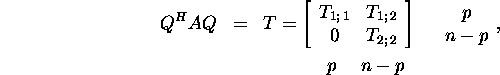
where ![]()
Proof. Let us consider for the matrix ![]() its QR factorization
its QR factorization 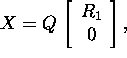 where
where ![]() and
and ![]() Substracting the factorization of the matrix X into equality (20),
we get
Substracting the factorization of the matrix X into equality (20),
we get
![]()
The spectres of the matrices QHAQ
and A coincide, i.e. ![]() Representing the matrix Ain form
Representing the matrix Ain form
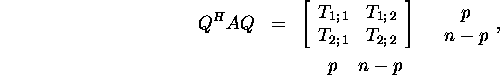
we find
![]()
Therefore, the proposition holds. ![]()
Remark 2.6.1. Proposition 2.6.4 makes it possible, if we know an invariant subspace of the given matrix, to transform it by unitary similarity transformations into a triangular block form.
Proposition
2.6.5 (Schur's decomposition). If ![]() then there exists a unitary matrix
then there exists a unitary matrix ![]() such that
such that
![]()
where ![]() and
and ![]() is a strictly upper triangular matrix, i.e., an upper triangular matrix
with zeros on the main diagonal. The matrix Q can be formed so that
the eigenvalues of the matrix A
are in the given order on the main diagonal of the matrix D.
is a strictly upper triangular matrix, i.e., an upper triangular matrix
with zeros on the main diagonal. The matrix Q can be formed so that
the eigenvalues of the matrix A
are in the given order on the main diagonal of the matrix D.
To prove this assertion we will use the method
of complete induction. As the assertion holds for n=1, the base
for the induction exists. We are going now to show the admissibility of
the induction steps. We suppose that the assertion holds for the matrices
which order is less or equal to k-1. Let us show that the assertion
will be valid for k, too. If ![]() and
and ![]() then, by lemma 2.6.4, choosing
then, by lemma 2.6.4, choosing ![]() ,
there exists a unitary matrix U such
that
,
there exists a unitary matrix U such
that
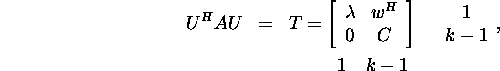
Since ![]() the assertion is valid for this matrix, i.e., there exists a unitary
matrix
the assertion is valid for this matrix, i.e., there exists a unitary
matrix ![]() such that
such that ![]() is an upper triangular matrix. If
is an upper triangular matrix. If ![]() then
then
![]()
![]()
![]()
and so the matrix QHAQ is an upper triangular matrix.
![]()
Example 2.6.2. Let
![]()
Let us show that Q is unitary matrix.
For this we, first, find the product QHAQ. The checking
of the matrix Q for unitarity gives:
![]()
![]()
![]()
Let us find the product
![]()
![]()
Consequently, we have obtained the Schur
decomposition of the matrix A.
Now (21) can be represnted in the form
AQ=QT. Replacing ![]() where the vectors
where the vectors ![]() are called Schur vectors, into the last
equality , we get
are called Schur vectors, into the last
equality , we get
![]()
or
![]()
![]()
or
![]()
From this equality it turns out that all subspaces ![]() (
k = 1: n) are invariant with respect to multiplication by the matrix A
on the left, and Schur vector
(
k = 1: n) are invariant with respect to multiplication by the matrix A
on the left, and Schur vector ![]() is an eigenvector of the matrix A
if and only if in the
is an eigenvector of the matrix A
if and only if in the ![]() -th
column of the matrix
-th
column of the matrix ![]() there are only zeros.
there are only zeros.
Definition 2.6.4. If
![]() and AHA=AAH, then A is called
a normal matrix.
and AHA=AAH, then A is called
a normal matrix.
Exercise 2.6.4.* Check the normality of A if
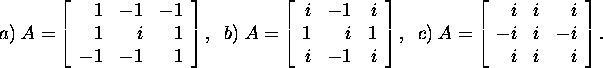
Proposition 2.6.6. A matrix ![]() is normal matrix if there exists a unitary
matrix
is normal matrix if there exists a unitary
matrix ![]() satisfying the condition
satisfying the condition ![]()
Proof. If the matrix A is unitarily similar
to the diagonal matrix D, then
![]()
![]()
and since diagonal matrices are commutative, then AHA=AAH
and the matrix A is normal . Vice versa, if the matrix A
is normal and the Schur
decomposition of this matrix is QHAQ=T, then
T is also normal because
![]()
and
![]()
Since a triangular matrix is normal only if
it is a diagonal matrix, then it has been proved that a unitary
matrix is similar to a diagonal matrix.
Proposition
2.6.7 (block-diagonal-decomposition). Let
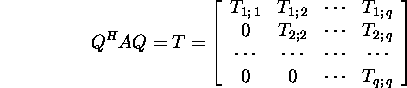
be the Schur decomposition of the
matrix ![]() , where the blocks
, where the blocks ![]() are square matrices. If
are square matrices. If ![]() then there exists a regular matrix
then there exists a regular matrix ![]()
![]() such that
such that
![]()
Corollary 2.6.1. If ![]() then there exists a regular matrix X such that
then there exists a regular matrix X such that
![]()
where ![]() ,
, ![]() and each
and each ![]() is a strictly upper triangular matrix.
is a strictly upper triangular matrix.
Proposition 2.6.8
(Jordan decomposition). If ![]() then there exists a regular matrix
then there exists a regular matrix ![]() such that
such that ![]() where
where
![]() ,
,
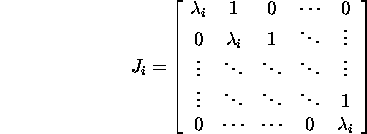
is an ![]() Jordan block,and the matrix J is called the Jordan normal form
of the matrix A .
Jordan block,and the matrix J is called the Jordan normal form
of the matrix A .
Proof. See Lankaster (1982, p. 143).
Example 2.6.3. Using ''Maple'' , we find the Jordan
decompositions A=XJX-1 of two matrices:
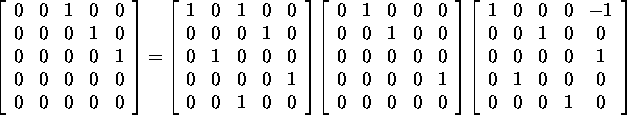
and
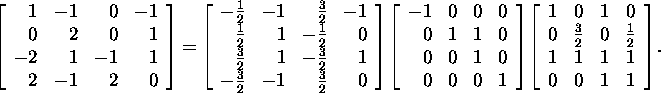
![]()
![]()
![]()