Let us consider an 
matrix
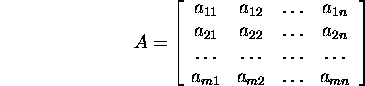
with real elements. The matrix A can be expressed both by the column-vectors
=
1 : n) of A or by the row-vectors 
=1
: m) by the transpose of A
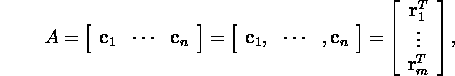
where 
and 
and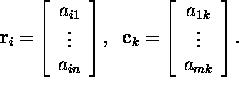 
Definition 2.4.1.
The subspace 
of the set 
of column-vectors of the matrix A is called the subspace of column-vectors
of the matrix A, and denoted by 
or ran(A).
Definition 2.4.2.
The subspace 
of the set 
of the row-vectors of the matrix A is called the subspace of
row-vectors of the matrix A, and denoted by 
or ran(AT).
Definition 2.4.3. The rank of the matrix A is the greatest natural number k, for which there exist a minor of order k different from zero. We denote the rank of A by rank(A).
Let rank(A)=r. Due to the theorem about the rank of the matrix, we get
Proposition 2.4.1.
The rank of the matrix is equal to the dimension of
the subspace of its row-vectors or column-vectors,
i.e.,
Definition 2.4.4. The (right)
null space of the matrix A is the set of all solutions
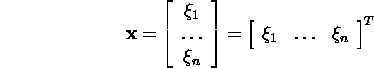
of the system of equations
It is a subspace,
denoted 
or null(A).
Proposition 2.4.2.
For every matrix 
with the rank r, it holds
Proof. The matrix of the system has the rank
r, and the number of variables in (4) equals n. Therefore,
the number of degrees of freedom of the system is n-r. The
number of degrees of freedom gives the dimension of the null
space. Thus, 
We can rewrite the system (4) in form
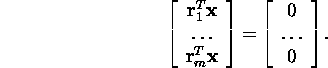
Therefore, 
=
1 : m), i.e., the row-vectors of A are orthogonal to any vector
of the null space
of the matrix A. Hence 
As, in addition, 
and 
and the space 
can be expressed by direct sum
Definition 2.4.5. The
(left) null space of the matrix A is the set of all solutions
of the system of equations
This subspace is denoted by 
or null(AT).
Proposition 2.4.3.
For every matrix
with the rank r, it holds
Proof. The matrix of the system AT
has the rank r, and, the number of variables
in (5) equals m. Therefore, the number of degrees of freedom of
the system is m-r and
The system (5) can be expressed in form
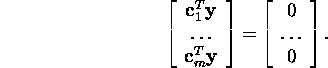
So 
=
1 : m) and 
As 
and 
and the space Rm can be expressed by direct sum
Example 2.4.1. Let us find the dimensions and bases
of the subspaces 
and
for the matrix
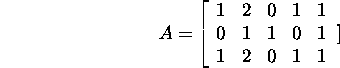
We will illustrate the assertion of propositions
2.4.2 and 2.4.3 in case of this example.
We start with the examination of the space .
Substracting from the second column of A two times the first column,
we get
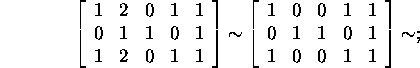
then substracting from the third column the new second one, from the forth
column the first one and from the fifth column the first one and the new
second one, we get
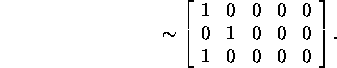
The symbol 
between the matrices marks that
is not changed. The last matrix has only two columns different from the
null vector 
The basis in the space
will be
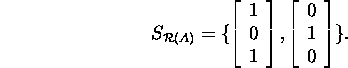
To describe the space ,
we solve system (5):
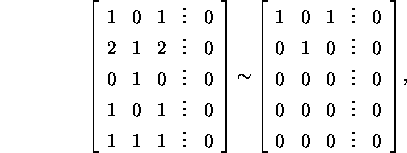
i.e.,
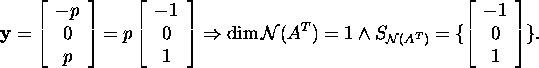
Let us check by scalar
product that 
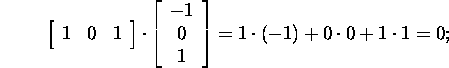
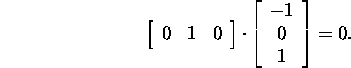
The union 
contains three linearly independent
vectors of 
.
These vectors form a basis in .
Thus, 
To describe the space
let us find its dimension and
basis:
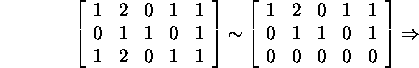
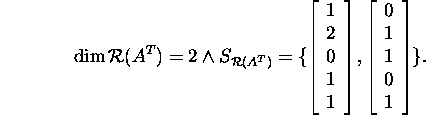
To describe the space ,
we solve system (4):
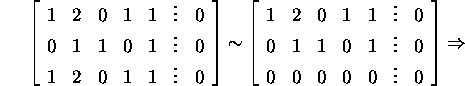
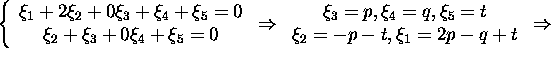
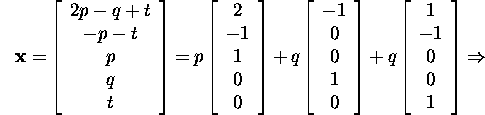
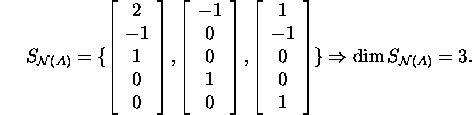
The vectors of the basis 
are orthogonal to the vectors
of the basis 
Thus, 
and the union 
forms a basis in 
Therefore
Problem 2.4.1. Let 
Show that 
Problem 2.4.2. Show that
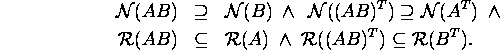
Problem 2.4.3.*
Find the dimensions and
bases of the subspaces
and
of the matrix A. Demonstrate the assertion of proposition
2.4.2 and 2.4.3 on the matrix A,
where
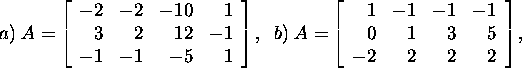
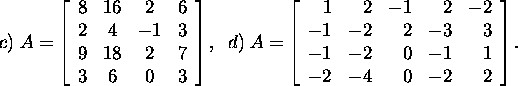
Problem 2.4.4.* Find the dimensions
and bases of the subspaces 
and 
of the product AB, where
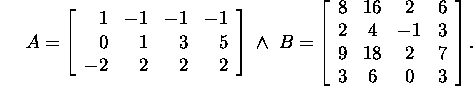
Compare the results obtained with the results of Problem
2.4.3* in case b) and c).