Norms and Condition Numbers of a Matrix

Definition 2.7.1. A mapping is called the norming of a matrix and obtained value the matrix norm if the following three conditions are satisfied:

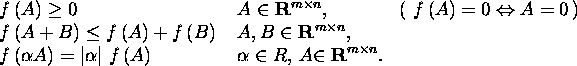
The matrix norm will be denoted

The most frequently used norms in linear algebra are the Frobenius norm
 
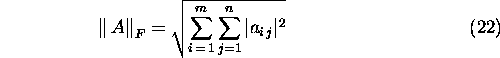
and the p-norms
 
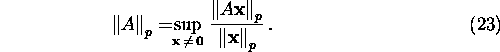
From (23) it follows that

or
 
Let us verify that p-norm satisfies the conditions of the matrix norm. We find that



further





and

Exercise 2.7.1. Verify that the Frobenius norm satisfies the conditions of the matrix norm.

Exercise 2.7.2.* Compute the Frobenius norm if

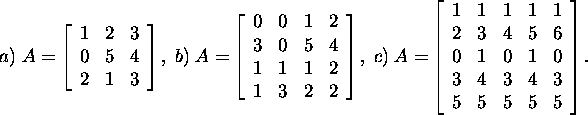
Definition 2.7.2. For the fixed matrix norm the value

is called the condition number corresponding to the regular square matrix

The condition number corresponding to the Frobenius norm will be denoted k_F(A) and the condition number corresponding to the p-norm will be denoted k_p(A). For a singular square matrix we will define

Exercise 2.7.2. Show that if then

Proposition 2.7.1. Rule (23) for the calculation of the norm can be transformed to the form
 

Proof. Using the third property of the norm and the homogeneity of multiplication of a vector by a matrix, we have

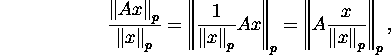
where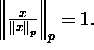

Proposition 2.7.2. If , and then

Proof. Using (24) and (25), we find that

Remark 2.7.1. Since then always .

Remark 2.7.2. For each and and for arbitrary vector norm on and on it holds the relation

where is a matrix norm defined by

Since the set is compact and is continuous, it follows that

for some with

Definiton 2.7.3.If k(A) is relativly small, then the matrix A is called a well-conditioned matrix, but if k(A) is great, then an ill-conditioned matrix.

Definition 2.7.4. A norm of the square matrix A is said to be consistent to the vector norm if

and it is submultiplicative, i.e.,

Definition 2.7.5. The norm of the square matrix, consistentto the vector norm is said to be subordinate to the vector norm if for any matrix A there exists a vector such that

Proposition 2.7.3. For arbitrary vector norm there exists at least one matrix norm subordinate (and thus at least one consistent ) to this vector norm, and this is

Remark 2.7.3. Not all matrix norms satisfy the submultiplicative property . For example, if we define , then for the matrices 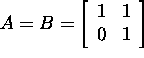we have and

Proposition 2.7.4. If , then the following relations between the matrix norms hold:
 

 








If and then

Prove the relation (27) . We have

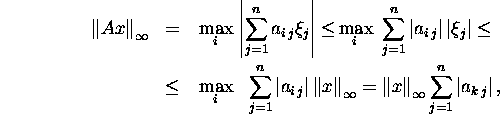
where we suppose that maximum has been gained if the index i obtains the value k . We have the estimation

Let

and

Since then

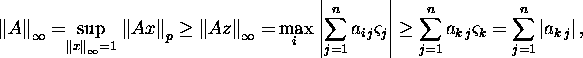
and thus

Example 2.7.1. Let us calculate the norms and for the matrix A if

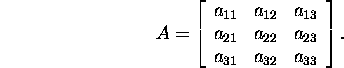
From (26) ja (27) we find that



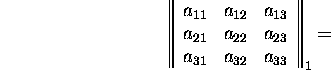
and

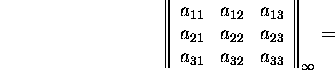
Example 2.7.2. Let us calculate the inverse matrix A^-1 of the matrix , the norms and the condition numbers of matrix A k₁(A), if

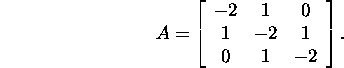
It follows that



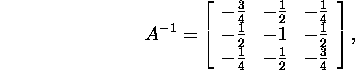
and

If formulae (26) and (27) enable to calculate easily 1-norm and norm, respectively, then the calculation of the 2-norm is more complicated. The matrix 2-norm is called also the matrix spectral norm.

Proposition 2.7.5. If then

i.e., is the square root of the largest eigenvalue of A^TA .

Proof. To calculate we find first Thus,

Let The matrix B is a symmetric matrix because

and







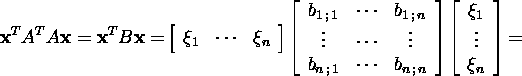
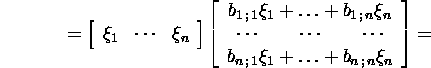
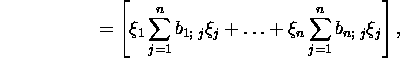
then is a function of n variables and



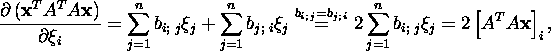
The problem of finding is a problem of finding the relative extremum. To solve our problem we form an auxiliary function

To find the stationary points of we form the system of equations:

i.e.,

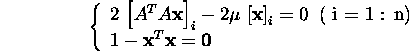
or

Thus, any stationary point for relative extremum is the normed vector corresponding to an eigenvalue of. Let us express from the relation

the eigenvalue We obtain that , where Comparing this result with the original formula for finding we notice that . Thus,

i.e., is the square root of the largest eigenvalue of A^TA .

Corollary 2.7.1. If matrix is symmetric, then

Example 2.7.3. Let us calculate the inverse matrix A^-1 of the matrix A, the norms and the condition numbers of the matrix A k₁(A), if

We obtain that

Example 2.7.4. Let us see how the almost singularity (the value of the determinant is close to zero) and ill condition of the matrix are related. For the matrix

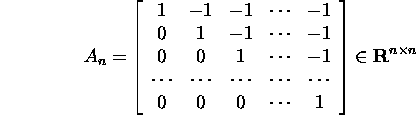
but In contrast, for the diagonal matrix

k_p(D_n)=1 but for an arbitrarily small . Exercise 2.7.4.* Find the inverse A^-1 of the matrix A, the norms and the condition numbers k₁(A), if
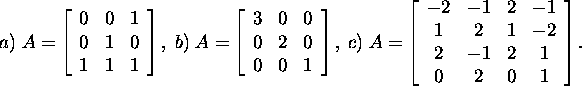