Definition 1.2.1. The set
of vectors of the vector
space 
(over the field 
)
that is a vector space will respect to vector addition and multiplication
by a number defined in the vector space
,
is called a subspace of the vector
space
and denoted 
Proposition 1.2.1
The set
of vectors of the vector space
is a subspace of the vector
space
if for each two vectors 
and each number 
vectors 
and 
belong to the set .
Proof. Necessity is obvious. To prove sufficiency,
we have to show that in our case conditions 1-8
of the vector spaces are satisfied.
Let us check condition 1. Let 
By assumption, 
.
As
is a vector space, then for
axiom 1 is satisfied, and then 
.
Therefore, for
axiom 1 is satisfied, too. Let us found the validity of condition 4. Let
By assumption, 
On the other hand, by preposition 1, in
the equality 
holds. Hence the inverse vector 
belongs to set
with the vector 
,
i.e., condition 4 is satisfied. Prove by yourselves the validity of condition
2, 3 and 5-8. 
Example 1.2.1. The vector
space 
over 
of all functions continouos on 
(example 1.1.3) is a subspace of vector
space 
As the sum of two functions continouos on the interval, and the product
of such a function by a number are functions continouos on this interval,
by proposition 1.2.1, 
is a subspace of the vector
space
Example 1.2.2. Let 
be the set of all polynomials 
of at most degree n with real coefficients. We define addition of
two polynomials and multiplication of a polynomial by a real number in
usual way. As the result, we get the vector
space
of polynomials of at most degree n. If we denote by 
the vector space of polynomials of
at most degree n defined on the interval ,
then
will be a subspace of vector
space 
Example 1.2.3.* Let us show that the
set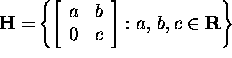 
is a subspace in the matrix vector
space 
The set 
is closed with respect to additism and multiplication by scalar since
and
Thus the set
is a subspace in the matrix vector
space
Problem 1.2.1.* Prove that the set of
all symmetric matrices form a subspace in the vector
space of all square matrices 
Proposition 1.2.2. If 
are subspaces of the vector
space ,
then the intersection 
of the subspaces is a subspace of the vector
space 
Prove!
Proposition 1.2.3. If 
are subspaces of the space
and
is the sum of these subspaces, then 
is a subspace in
Definition 1.2.2. If each 
can be expressed uniquely in the form 
then we say that
is the direct sum of subspaces
and it denoted 
Definition 1.2.3.Each
element of the space
that can be expressed as 
where 
is called a linear combination of the elements 
of the vector space
(over the field ).
Definition 1.2.4.The set of
all possible linear combination of the
set Z is called the span of the set 
Example 1.2.4. Let 
and 
Then 
Prove!
Proposition 1.2.4. The set 
of the set 
is the least subspace that contain the set 
Proof. First, let us prove that
is a subspace of the space .
It is sufficient, by proposition 1.2.1,
to show that
is closed with respect to vector addition and multiplication of the vector
by a number:
Thus,
is a subspace of the space .
Let us show that
is the least subspace of the space
that contains the set Z. Let 
be some subspace of the space
for which 
As 
and
is a subspace, the arbitrary linear combination of the elements os the
set Z belongs to the subspace 
Therefore,
as the set of all such linear combinations
belongs to the space
Corollary 1.2.1. A subset
of the vector space
is a subspace if it coincides with its span, i.e.,
Problem 1.2.2.* Does the vector 
belong to the subspace 
,
when
