Let us consider a matrix ![]() and a function of complex variable
and a function of complex variable
![]()
There is a lot of possisilities to define a function of matrix f(A)
starting from the function of complex variable f(z). The
simplest of these possibilities seems to be the substituting the variable
"z" by the variable "A". For example,
![]()
and
![]()
as well
![]()
![]()
![]()
![]()
It turns out that this approach is not very practical for solving problems.
Definition 2.9.1. If
![]() , f(z) is analytic in the open domain
, f(z) is analytic in the open domain ![]() ,
, ![]() is a closed simple line (does not cut itself) in
is a closed simple line (does not cut itself) in ![]() and the spectrum
and the spectrum ![]() of the matrix A is included in domain
of the matrix A is included in domain ![]() enfolded by
enfolded by ![]() ,
then
,
then
![]()
where the integral is applied to the matrix by its elements.
Remark 2.9.1. Formula (28) is an analogue to the Cauchy integral formula proved for the functions of complex variable.
Example 2.9.1. Let f(z)=z
and 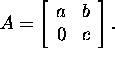 Check how to calculate by rule (28). Since
Check how to calculate by rule (28). Since ![]() and
and ![]() are the eigenvalues of A ,
then let us choose the line
are the eigenvalues of A ,
then let us choose the line ![]() where
where ![]() The function f(z)=z is analytic in domain
The function f(z)=z is analytic in domain ![]() First we find
First we find
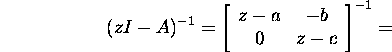
![]()
and then
![]()
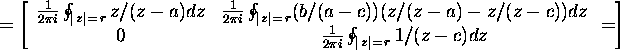
![]()
Proposition 2.9.1.
If ![]() then
then
![]()
where ![]() is a vector in space
is a vector in space ![]() whose k-th component is one and the remaining ones are zeros.
whose k-th component is one and the remaining ones are zeros.
Proof. Let ![]() Then,
Then,
![]()
Since the matrix is integrated by elements, we obtain that
![]()
Proposition 2.9.2. If ![]() , there
, there ![]() i.e., the conditions of definition 2.9.1
are satisfied, and
i.e., the conditions of definition 2.9.1
are satisfied, and
![]()
then
![]()
Proof. From (28) , (29) and XX-1=I
we find that
![]()
![]()
Since
![]()
and
![]()
![]()
![]()
then
![]()
that was to be proved.
Proposition 2.9.3. If
![]() and
and ![]() is the Jordan normal form
of the matrix A , where
is the Jordan normal form
of the matrix A , where
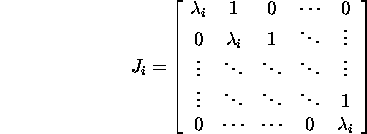
is an ![]() Jordan block,
Jordan block, ![]() and f(z) is analytic on an open set that includes the spectre
and f(z) is analytic on an open set that includes the spectre
![]() of the matrix A, then
of the matrix A, then
![]()
where
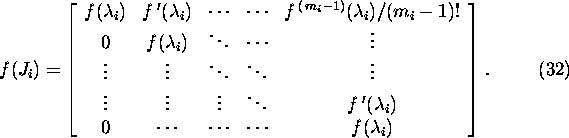
Prooof. Using Proposition 2.9.2
it is sufficient to consider only the value F(G), where ![]() is a
is a ![]() Jordan block and
Jordan block and ![]() Let the matrix zI-G be regular. Since
Let the matrix zI-G be regular. Since
![]()
then
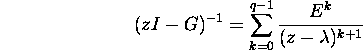
and
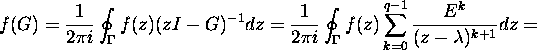
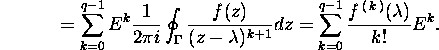
Now, taking into account the condition ![]() the assertion holds.
the assertion holds.
Example 2.9.2. Find ![]() if
if
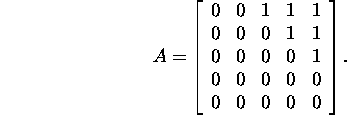
Since ![]() and the function
and the function ![]() is analytic in the neighbourhood of 0 , then for the calculation of
is analytic in the neighbourhood of 0 , then for the calculation of ![]() we can apply the algorithm given in Proposition
2.9.3. We use for the calculation of Jordan
decomposition of the matrix A the ''Maple'':
we can apply the algorithm given in Proposition
2.9.3. We use for the calculation of Jordan
decomposition of the matrix A the ''Maple'':
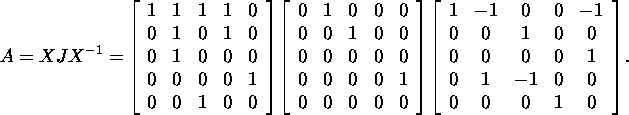
Therefore, J=diag(J1,J2),where
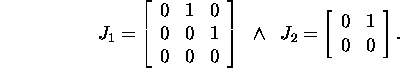
Using (3), we find the matrices ![]() and
and ![]() :
:
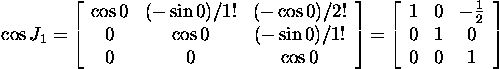
and
![]()
After that, using (2), we find the matrix wanted:
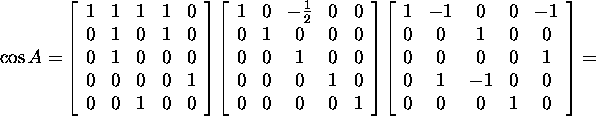
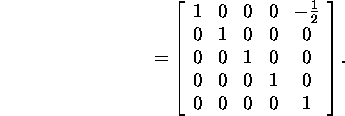
Corollary 2.9.1. If
![]() ,
, ![]() and there
and there ![]() then
then
![]()
Proof. This is a special case of Proposition
2.9.3. All the Jordan blocks
are ![]()
Example 2.9.3. If ![]()
![]() are the eigenvalues of the matrix
are the eigenvalues of the matrix
![]() and
and ![]() are the corresponding linearly
indipendent eigenvectors , i.e.,
are the corresponding linearly
indipendent eigenvectors , i.e.,
![]() generate a basis in
generate a basis in ![]() then
then ![]() and from analyticity of
and from analyticity of ![]()
![]()
![]() in the whole finite part of complex plane it follows that
in the whole finite part of complex plane it follows that
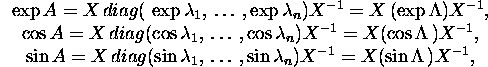
where ![]() and
and
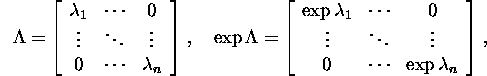
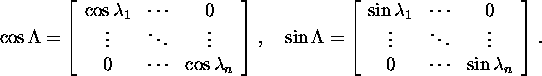
Next we consider the problem arising in the approximation of the function f(A) by the function g(A). This kind of problem arises, for example, if we replace f(A) with its Taylor polynomial of degree q.
Proposition 2.9.4.
Let ![]() ,
,
![]() where
where
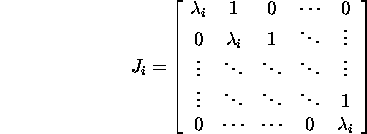
is an ![]() Jordan block and
Jordan block and ![]() If the functions f(z) and g(z) are analytic
on an open set containing the spectre
If the functions f(z) and g(z) are analytic
on an open set containing the spectre
![]() of the matrix A, then
of the matrix A, then
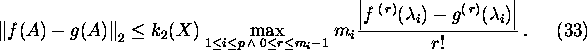
Proof. Choosing ![]() we
have
we
have
![]()
![]()
Using Proposition 2.9.3 and inequality
![]() we find that
we find that
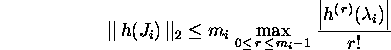
and thus, the assertion holds.
Example 2.9.4. Let
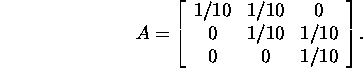
We estimate the difference ![]()
Since ![]() and the functions
and the functions ![]() and g(z)=z are analytic in the neighbourhood of .1,then
we can apply the estimation (33) obtained in Proposition 2.9.4. First,
we use ''Maple'' for finding the Jordan
decomposition of the matrix A:
and g(z)=z are analytic in the neighbourhood of .1,then
we can apply the estimation (33) obtained in Proposition 2.9.4. First,
we use ''Maple'' for finding the Jordan
decomposition of the matrix A:
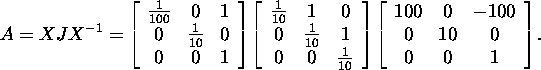
Hence, there is only one Jordan
block in the Jordan decomposition
of the matrix A, i.e.
![]()
Second, we use ''Maple'' for finding the condition number of X:
![]()
Since
![]()
![]()
and
![]()
then, by estimation (30), we have that
![]()
It is known that matrix X in the Jordan
decomposition of A is not uniquely determined. We try to choose
the matrix X so that the condition
number k2(X) should be minimal. Applying the
Filipov algorithm to find the Jordan
decomposition of A (see Proposition
2.5.2.1), we obtain that
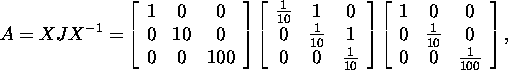
where
![]()
It turns out that
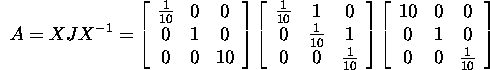
is also a Jordan decomposition
of A, where
![]()
Therefore, the best estimation we can have by Proposition
2.9.4 is
![]()
Otherwise, in this example for calculating ![]() there is applicable the algorithm given in Proposition
2.9.3. Using the formula (32), we have that
there is applicable the algorithm given in Proposition
2.9.3. Using the formula (32), we have that
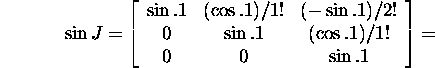
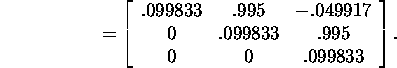
By formula (31) we calculate the value of the function
in question:
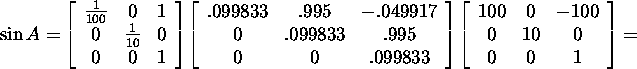
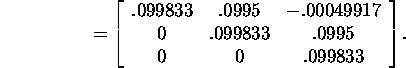
Hence,
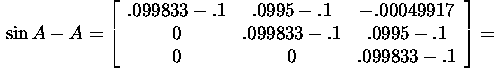
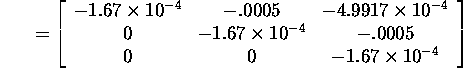
and
![]()
As a result of this example, we can assert that estimation
(33) proved in Proposition 2.9.5 is quite rough.
Proposition 2.9.5.
If the Maclaurin expansion of the function f(z)
![]()
is convergent in the circle containing the spectrum ![]() of the matrix
of the matrix ![]() then
then
![]()
Prove this assertion with an additioal assumption
that the matrix A has a basis consisting of its eigenvectors. In
this case, by Corollary 2.9.1,
![]()
![]()
![]()
Proposition 2.9.6.
If the Maclaurin series of the function f(z)
![]()
is convergent in the circle containing the spectrum ![]() of the matrix
of the matrix ![]() then
then
![]()
Proof. Let us define the matrix E(s)
by
![]()
If ![]()
![]() ,
then
,
then ![]() is analytic, and therefore,
is analytic, and therefore,
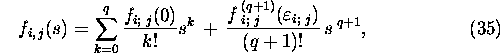
where ![]() By
comparing the powers of the variable s in (34)
and (35), we conclude that
By
comparing the powers of the variable s in (34)
and (35), we conclude that ![]() has the form
has the form
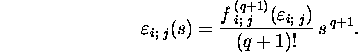
If ![]() then
then
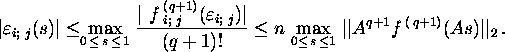
Exercise 2.9.1. Prove that for an arbitrary matrix
![]() there hold
there hold
![]()
and
![]()
Exercise 2.9.2. Apply Proposition
2.9.6 to the estimation of the errors in the approximate equalities
![]()
and
![]()
Proposition 2.9.7 (Sylvester
theorem). If all eigenvalues
![]() of the matrix
of the matrix ![]() are different, then
are different, then
![]()
or
![]()
where ![]()
![]() is the determinant obtained from the Vandermonde
determinant
is the determinant obtained from the Vandermonde
determinant
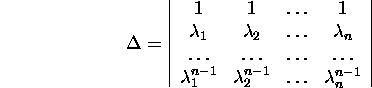
by replacing the k-th row vector
![]()
by the vector
![]()
Example 2.9.4. Calculate ![]() if
if 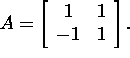
First we find the eigenvalues of A:
![]()
Then we use formula (36):
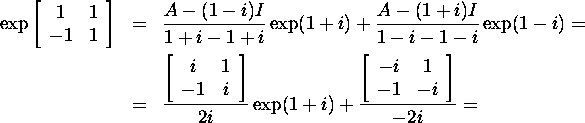
![]()
Now applying (37), we have
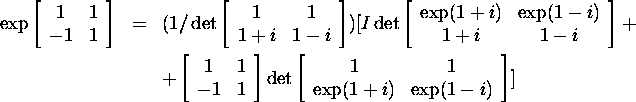
![]()
![]()
We solve this problem once more using the formula ![]() where S is the matrix formed of the eigenvalues
of A. Find the eigenvalues of A:
where S is the matrix formed of the eigenvalues
of A. Find the eigenvalues of A:
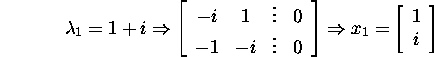
and
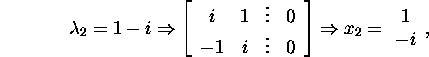
and the matrix
![]()
Hence
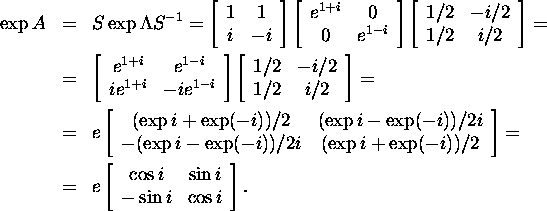
![]()
![]()
![]()