Peatüki algus: Numbriline stabiilsus
Eelmine: Numbriline stabiilsus
Järgmine: Taylori arendus

Definitsioon 8.1.1. Maatriksi A astak defineeritakse valemiga

Näide 8.1.1.^* Leiame maatriksi

-astaku, kui
Ilmselt

Kui peaks paika seos

siis

Kuna

siis



kus ja on maatriksi

omaväärtused. Järelikult ja ning

See on vastuolu ja see tähendab, et Näitame, et Tõepoolest, maatriksi

korral ja



kus ja on maatriksi

omaväärtused. Seega ja ning

See aga tähendab, et

Lause 8.1.1. Olgu maatriksi singulaarlahutus. Kui k<r=rank(A) ja

siis

Tõestus. Kuna











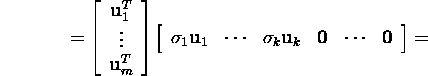
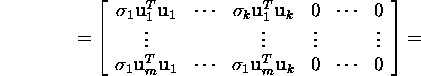
ja

kusjuures Kuna maatriksi A-A_k eukleidiline norm võrdub maatriksi U^T(A-A_k)V suurima elemendiga, siis

Olgu maatriks, mille korral rank(B)=k. Võime leida sellised ortonormaalsed vektorid et maatriksi B nullruum on vektorite lineaarne kate, so

Kuna ruumis on n+1 vektorit lineaarselt sõltuvad, siis

Kui on ühikvektor (eukleidilise normi järgi) sellest ühisosast, siis ja



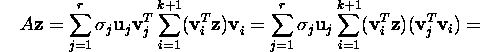
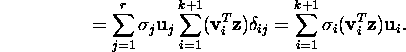
Järelikult,

Järeldus 8.1.1. Kui maatriks on regulaarne, siis maatriksi A vähim singulaararv näitab maatriksi A kaugust lähimast singulaarmaatriksist.

Ülesanne 8.1.1.^* Kasutage näites 8.1.1 esitatud ülesande lahendamiseks järeldust 8.1.2.

Lause 8.1.2. Kui

on regulaarse maatriksi singulaarlahutus, siis süsteemi (1) lahend avaldub kujul
 

Tõestus. Kontrollime lause väite õigsust:

Järeldus 8.1.2. Lahendi esitusest kujul (2) selgub, et maatriksi A elementide väikesed hälbed võivad põhjustada lahendi suuri hälbeid, kui on väike.

Näide 8.1.2.^* Kumba süsteemi, kas

või

süsteemimaatriksi elementide väikesed hälbed võivad põhjustada lahendi suuremaid hälbeid?
Leiame paketi ''Maple'' abil mõlema süsteemimaatriksi singulaarlahutuse:

ja

Näeme, et esimese süsteemi süsteemimaatriksi vähim singulaarväärtus on sada korda suurem kui teise süsteemi süsteemimaatriksi vähim singulaarväärtus. Seega järelduse 8.1.2 põhjal võime väita, et esimene süsteem on stabiilsem kui teine, so teise süsteemi süsteemimaatriksi elementide väikesed hälbed võivad põhjustada lahendi suuremaid hälbeid kui esimese süsteemi süsteemimaatriksi elementide sama järku hälbed.

Ülesanne 8.1.2.^* Kumb süsteemidest, kas

või

on stabiilsem?