Peatüki algus: Singulaarlahutus
Eelmine: Singulaarlahutus
Järgmine: Singulaarlahutuse omadused

Lause 3.1.1. Kui maatriksil on ortonormeeritud veerud, siis leidub selline et on ortogonaalmaatriks, kusjuures maatriksi V₁ veeruvektorite lineaarse katte ortogonaalne täiend võrdub maatriksi V₂ veeruvektorite lineaarse kattega st

Tõestus põhineb Gram-Schmidt'i ortogonaliseerimisprotsessil.

Lause 3.1.2. Kui ja on ortonormeeritud veergudega maatriks, siis

Tõestus. Ortonormeeritud veergudega maatriksi korral ja

Lause 3.1.3. Olgu Kui ja on ortogonaalmaatriksid, siis

ja
 

Tõestame seose (1):

Lause 3.1.4 (teoreem singulaarlahutuse olemasolust). Kui siis leiduvad sellised ortogonaalsed maatriksid

ja

et
 
kusjuures

Tõestus. Maatriksi 2-normi definitsiooni põhjal leiduvad sellised vektorid ja et kusjuures ning Lause 3.1.1 põhjal leiduvad sellised maatriksid ja et ja on ortogonaalmaatriksid. Sellise tähistuse korral saame, et





kus ja B=U₂^TAV₂. Kuna

siis

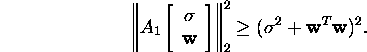
Teisalt,

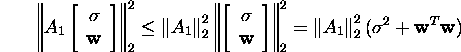
ja seega

Lause 3.1.3 põhjal leiame, et Järelikult, 0 ja Saame, et

ehk

ja

Seega maatriksid A^TA ja 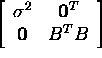on sarnased ja neil on samad omaväärtused. Järelikult,

kusjuures kui on maatriksi A^TA suurim omaväärtus. Nendime, et tänu maatriksi A^TA sümmeetrilisusele on kõik maatriksi A^TA omaväärtused mittenegatiivsed. Arutelu, mida kasutasime maatriksi A korral, kasutame järgneval etapil maatriksi B korral, jne. Seega piki maatriksi peadiagonaali paigutuvad ruutjuured maatriksi A^TA omaväärtustest, täpsemalt esimesed kahanevas järjestuses.

Definitsioon 3.1.1. Seost kujul (2) nimetatakse maatriksi singulaarlahutuseks. Seoses (2) esineva maatriksi peadiagonaali elemente nimetatakse maatriksi A singulaarväärtusteks.