Definition 8.1.1. The 
rank
of the matrix A is defined by the formula
Example 8.1.1.*
Let us find the 
-rank
of the matrix
if 
Evidently,
If the equality
holds, then
Since
then
where 
and 
are the eigenvalues of the
matrix
Therefore, 
and 
and
This is a contradiction, and it means that 
Let us show that 
Really, for the matrix
rank(B)=1 and
where
and
are the eigenvalues of the
matrix
Thus, 
and 
,
and
But this means that
Proposition 8.1.1.
Let 
be the singular value decomposition
of a matrix 
.
If k<r=rank(A) and
then
Proof. Since
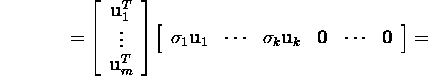
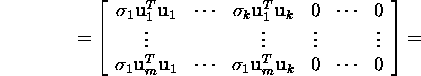
and
while 
Since the Euclid norm of the matrix A-Ak equals
the greatest entry of the matrix UT(A-Ak)V,
then
Let 
be a matrix for which rank(B)=k. We can find the orthonormal
vectors 
such that the null space of
the matrix B is a linear span
of the vectors 
,
i.e.,
Since in the space 
n+1 vectors are linearly
dependent, then
If 
is a unit vector (by the Euclidean norm) from this intersection, then 
and
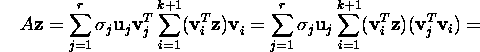
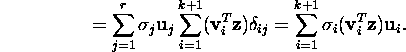
Hence
Corollary 8.1.1. If
the matrix 
is regular, then the least singular
value 
of the matrix A shows the distance of the matrix A from the
nearest singular matrix.
Problem 8.1.1.* Use corollary 8.1.2 to solve the problem given in example 8.1.1.
Proposition 8.1.2.
If
is the singular value decomposition
of the regular matrix ,
then the solution 
of system (1) can be expressed in the form
Proof. Let us check the correctness of the assertion
of the proposition:
Corollary 8.1.3. From
the representation of the solution in form (2) it appears
that small deviations of the entries of the matrix A could cause
great deviations of the solution
if
is small.
Example 8.1.2.* For which system
or
small deviations of the entries of the system matrix can cause greater
deviations of the solution ?
Applying the package ``Maple'', we find the singular
value decomposition of both system matrices:
and
We see that the least singular value
of the first system matrix is hundred times smaller than the least singular
value of the second system matrix. Therefore, in virtue of corollary
8.1.3, we can state that the first system is more stable than the second
one, i.e., small deviations of the entries of the second system matrix
can cause greater deviations of the solution
than the deviation of the same order of the entries of the first system
matrix.
Problem 8.1.2.* What of two systems
or
is more stable?
then 