Existence of Singular Value Decomposition

Proposition 3.1.1. If has orthonormal columns, then there exists such that is orthogonal, where the orthogonal complement of the span of column vectors of the matrix V₁ is equal to the span of the column vectors of the matrix V₂ , i.e.,

Proof is basing on the Gram-Schmidt orthogonalization.

Proposition 3.1.2. If and has orthonormal columns, then

Proof. If has orthonormal columns, then and

Proposition 3.1.3. Let If and are orthogonal, then

and
 

Prove relation (1):

Proposition 3.1.4 (existence theorem of the singular value decomposition). If then there exist orthogonal matrices

and

such that
 
with

Proof. By the definition of the matrix 2-norm there exist the vectors and such that where and By Proposition 3.1.1, there exist the matrices and such that and are orthogonal. Using this notation, we obtain that





with and B=U₂^TAV₂. Since

then

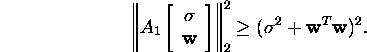
On the other hand,

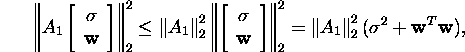
and therefore,

By Proposition 3.1.3, we find that Consequently, 0 and We obtain that

or

and

Thus, the matrices A^TA and 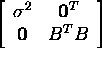are similar, and they have the same eigenvalues. Consequently,

where as is the greatest eigenvalue of A^TA. Note that since A^TA is symmetric then all eigenvalues of A^TA are non-negative. Reasoning used for the matrix A we shall use in the next step for the matrix B etc. So, on the main diagonal of there are the square roots of the eigenvalues of A^TA , more exactly, the first of them in descending order.

Definition 3.1.1. The relation in form (2) is called the singular value decomposition of the matrix The elements = on the main diagonal of are called the singular values of the matrix A.