Definition 1.6.1. The
vectors 
and 
of the vector space with scalar
product 
are called orthogonal if 
We write 
to indicate the orthogonality of vectors
and 
A vector
of the vector space
is called orthogonal to the set 
if 
Problem 1.6.1.* Find all vectors that
are orthogonal both to the vector 
and 
Definition 1.6.2. The
sets Y and Z of the vector
space
are called orthogonal if 
and 
Definition 1.6.3. A
sequence 
of vectors of the vector space
with scalar product
is called a Cauchy sequence if for any 
there is a natural number n0 such that for all 
and n>n0
Definition 1.6.4. A
vector space with scalar product
is called complete if every Cauchy sequence
is convergent to a point of the space .
Definition 1.6.5. A
vector space with complex scalar product is called a Hilbert space
if it turns out to be complete with respect to
the convergence by the norm
.
Proposition 1.6.1. The space 
with the scalar product
is a Hilbert space.
Proposition 1.6.2. The space 
of all square-integrable functions on the interval 
with the scalar product
is a Hilbert space.
Proposition 1.6.3. Orthogonality
of vectors in the vector space
with scalar product
has the following properties (1-4):
1. 
2. 
3. 
4. 
orthogonality of vectors in a Hilbert
space has an additional property:
5. 
Let us prove these assertions:
Definition 1.6.6. The
orthogonal complement of the set
is the set 
of all vectors of the space
that are orthogonal to the set Y, i.e.,
Problem 1.6.2.* Let 
Find the orthogonal complement of the set
U.
Proposition 1.6.4. If
is a vector space with scalar product, 
and 
then 
If, in addition,
is complete, i.e., is a Hilbert space, then 
Proof. By assertions 3 and 4 of proposition
1.6.3, 
.
If 
i.e., 
such that 
then, due to the orthogonality 
and assertion 5 of proposition 1.6.3, we get ,
i.e., 
Proposition 1.6.5. The
orthogonal complement
of the set
is a subspace of the space 
The orthogonal complement
of the set 
is a closed subspace of the Hilbert space 
i.e.,
is a subspace of the space
that contains all its boundary points.
Proof. Due to the proposition
1.2.1, it is sufficient for the proof of the first assertion of proposition
1.6.5 to show that
is closed with respect to vector addition and scalar multiplication. It
will follow from assertion 5 of the same proposition, it holds the second
assertion of proposition 1.6.5 too.
Proposition 1.6.6. If Y
is a closed subspace of the Hilbert
space
then each 
can be expressed uniquely as the sum 
,
Corollary 1.6.1. If 
is a closed subspace of the Hilbert
space, then the space
can be presented as the direct sum 
of the closed subspaces 
and 
,
and
Definition 1.6.7. The distance
of the vector
of the Hilbert space
from the subspace 
is defined by the formula
Proposition 1.6.7. If
is a closed subspace of the Hilbert
space
and ,
then there exist a uniquely defined 
such that 
Definition 1.6.8. The
vector
in proposition 1.6.7 is called the orthogonal
projection of
onto the subspace Y.
Definition 1.6.9.
A vector system 
is called orthogonal if 
where 
is the Kronecker delta. The vector system
is called orthonormal if 
.
Example 1.6.1. The vector system 
(
k = 1 : n), where 
is orthonormal in .
Example 1.6.2. The vector system
is orthonormal in 
Example 1.6.3. The vector system 
is orhtonormal in 
Truely,
Proposition 1.6.8. (Gram-Schmidt
orthogonalization theorem). If 
is a linearly independent
vector system in the vector
space with scalar product ,
then there exist an orthonormal system
such that 
Let us prove this assertion by complite induction.
In the case k=1, we define 
and, obviously, 
So we have shown the existence of the induction base. We have to show the
admissabily of the induction step. Let us assume that the proposition holds
for k=i-1, i.e., there exists an orthonormal
system 
such that 
Now we consider the vector
Let us choose the coefficients 
1:
i-1) so that 
=1:
i-1), i.e, 
We get i-1 conditions:
ehk 
=1: i-1).
Thus,
Now we chose 
Since
we get, by the construction of vectors 
and 
,
Hence
From the representation of the vector 
we see that 
is a linear combination of vectors 
Thus,
Finally,
Example 1.6.4. Given a vector system 
in 
,
where
Find such an orthogonal system
,
for which
To apply the orthogonalization process of proposition
1.6.8, we check first the system
for the linearly independence
(one can omit this process, too, because the situation will be clear in
the course of the orthogonalization:
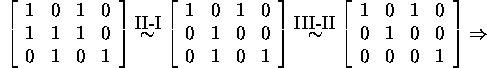
the system
is linearly independent.
Now we find
For 
we get:
As 
The vector 
can be expressed in the form:
Thus,
Example 1.6.5. Given a linearly
independent vector system
in 
,
where 
and 
Find an orthogonal system ,
such that
Check that the system
is linearly independent.
The first vector is
The vector
can be expressed in the form:
Thus,
The vector
can be expressed in the form:
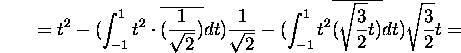
Therefore,
The functions 
and 
are the normed Legendre polynomials on [-1;1].
Problem 1.6.3. Show that a vector system 
with pairwise orthogonal elements is linearly
independent.