We can obtain the exact evaluation of the sensibility
of system (1) using the system depending on
a parameter
where 
,
and 
If A is a regular matrix, then 
is a differentiable function of the parameter 
in some neighbourhood of the value 0. Differentiating the both sides of
equality (3) with respect to the parameter ,
we get
and
It follows from relation (4) that
Let us write the first order Taylor formula for the
function
As the result, we obtain for arbitrary vector norm and for the matrix norm
corresponding to it
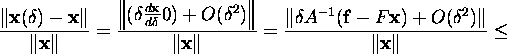
Taking into account that from relation (1)
it follows 
we obtain the evaluation
or
where 
and 
are the relative
errors of the matrix A and the vector 
,
respectively.
Proposition 8.2.1.
If 
is a regular matrix, then the relative
error 
of the solution of the linear system (1) corresponding
to the relative error 
of the matrix A and the relative
error 
of the vector
is given by
Corollary 8.2.1. In
case of the Euklidean norm it holds the estimation
Proof. The relation 
holds. As the matrix A is regular, it follows from its singular
value decomposition 
that 
where 
Since 
then 
and
Example 8.2.1.* Let us estimate the
relative error
of the solution 
of the system 
in case of the Euclidean norm if
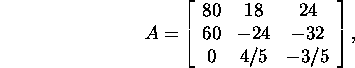
and 
Let us find the singular decomposition
of the matrix A
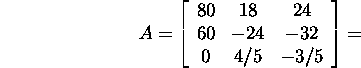
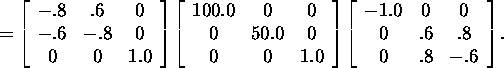
In virtue of corollary 8.2.1, we can state
Problem 8.2.1.* Estimate the relative
error
of the solution
of the system
in case of the Euclidean norm if
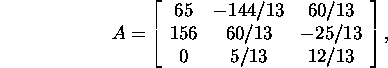
and 
Remark 8.2.1. Kahan (1966) proved that
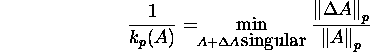
and Rice (1966) proved that
