Peatüki algus: Lineaarsete algebraliste võrrandisüsteemide lahendamise
Eelmine: Positiivselt poolmääratud maatriksid
Järgmine: Lintmaatriksitega süsteemid

Maatriksi polaarlahutus ja ruutjuurte meetod

Lause 6.4.1 (maatriksi kompaktsest singulaarlahutusest). Kui maatriksi tex2html_wrap_inline1933 tex2html_wrap_inline1935 singulaarlahutuseks on tex2html_wrap_inline1937 kus tex2html_wrap_inline1939 ja tex2html_wrap_inline1941 on ortogonaalmaatriksid ning tex2html_wrap_inline1943 siis selle maatriksi A kompaktseks singulaarlahutuseks on
displaymath1867
kus U1=U(: ,1:n) ja tex2html_wrap_inline1951 :).

Tõestus. Kui kasutada maatriksite U ja V esitust veeruvektorite abil
displaymath1868
ja
displaymath1869
siis
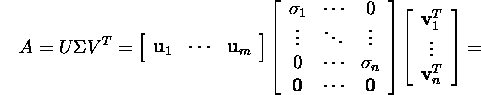
displaymath1870

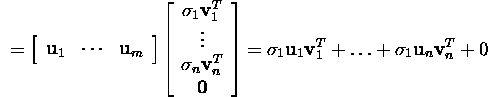
displaymath1871
ning
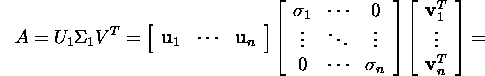
displaymath1872

displaymath1873

Näide 6.4.1. Leida maatriksi
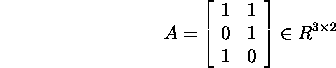
displaymath1874
kompaktne singulaarlahutus.

Maatriksi A singulaarlahutus tex2html_wrap_inline1961 on leitud näites 3.3.1. Selleks on
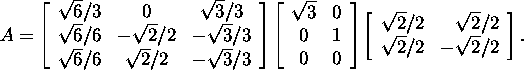
displaymath1875
Lause 6.4.1 põhjal on maatriksi A kompaktne singulaarlahutus kujul
displaymath1867
kus U1=U(: ,1:n) ja tex2html_wrap_inline1951 :), st
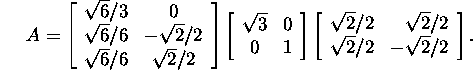
displaymath1877

Lause 6.4.2. Kui maatriksi tex2html_wrap_inline1933 kompaktseks singulaarlahutuseks on
displaymath1867
siis maatriks A on esitatav kujul
 equation801
kus tex2html_wrap_inline1977 on ortonormeeritud veergudega maatriks ja tex2html_wrap_inline1979 on positiivselt poolmääratud maatriks.

Tõestus. Kuna tex2html_wrap_inline1981 siis
displaymath1879
Kontrollime lause väidete õigsust. Esiteks, Z on ortonormeeritud veergudega maatriks, sest
displaymath1880
Teiseks, tex2html_wrap_inline1979 on positiivselt poolmääratud maatriks, sest
displaymath1881
kus tex2html_wrap_inline1987

Definitsioon 6.4.1. Maatriksi tex2html_wrap_inline1933 lahutust kujul (12) nimetatakse polaarlahutuseks.

Näide 6.4.2. Leida maatriksi
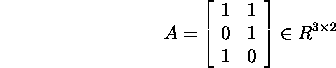
displaymath1874
polaarlahutus.

Näites 6.4.1 on leitud maatriksi A kompaktne singulaarlahutus tex2html_wrap_inline1993 Leiame maatriksi A polaarlahutuses (12) esinevad tegurid Z ja P:
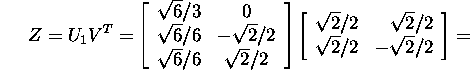
displaymath1883

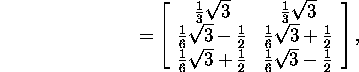
displaymath1884

displaymath1885

displaymath1886
Järelikult, maatriksi A polaarlahutuseks on


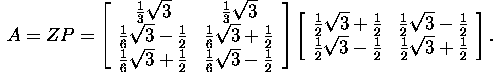
displaymath1887

Ülesanne 6.4.1.* Leidke maatriksi
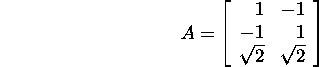
displaymath464
polaarlahutus.

Definitsioon 6.4.2. Otex2html_wrap_inline2003u tex2html_wrap_inline2005 Kui maatriks tex2html_wrap_inline2007 rahuldab võrrandit X2=A, siis maatriksit X nimetatakse ruutjuureks maatriksist A.

Lause 6.4.3. Kui
displaymath1888
on sümmeetrilise positiivselt poolmääratud maatriksi tex2html_wrap_inline1495 Cholesky lahutus ja
displaymath1889
on maatriksi G singulaarlahutus ning
displaymath1890
siis
displaymath1891
st maatriks X on ruutjuur maatriksist A, kusjuures X on sümmeetriline positiivselt poolmääratud maatriks. Leidub ainult üks X.

Tõestus. Leiame, et
displaymath1892

displaymath1893
Näidake, et maatriks X on üheselt määratud sümmeetriline positiivselt poolmääratud maatriks! tex2html_wrap_inline1519

Näide 6.4.3. Leime ruutjuure maatriksist
displaymath1894

Maatriks A on sümmeetriline ja positiivselt poolmääratud (vaadake näidet 6.3.1) ning
displaymath1895
Kuna
displaymath1896
siis
displaymath1897

displaymath1898

displaymath1899

Ülesanne 6.4.2.* Leidke ruutjuur maatriksist
displaymath465