Peatüki algus: Singulaarlahutus
Eelmine: Singulaarlahutuse omadused
Järgmine: Pseudo-pöördmaatriks

Algoritm 3.3.1. Maatriksi singulaarlahutuse (2) leidmiseks tuleb:

I Leida maatriksi A^TA omaväärtused ja paigutada need kahanemise järjekorras.

II Leida maatriksi A^TA nullist erinevate omaväärtuste arv r.

III Leida saadud omaväärtustele vastavad maatriksi A^TA ortonormeeritud omavektorid ja paigutada need samas järjekorras maatriksi veeruvektoreiks.

IV Moodustada diagonaalmaatriks mille peadiagonaalile paigutada ruutjuured punktis I saadud maatriksi esimesest omaväärtusest kahanevas järjestuses.

V Leida maatriksi esimesed veeruvektorid:
 

VI Lisada maatriksisse U ülejäänud m-r veeruvektorit Gram-Schmidt'i ortogonaliseerimisprotsessi abil.

Näide 3.3.1. Leiame maatriksi

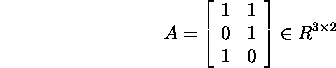
singulaarlahutuse.

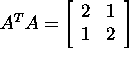I Leiame omaväärtused:

II Leiame maatriksi A^TA nullist erinevate omaväärtuste arvu: r=2 .

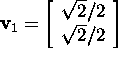III Leiame maatriksi A^TA omaväärtustele ja v astavad ortonormeeritud omavektorid ja 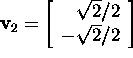ning moodustame maatriksi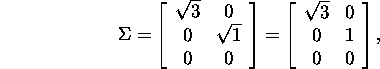

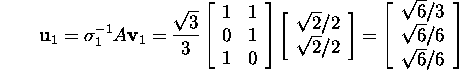
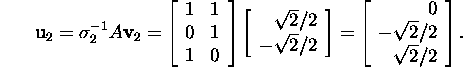
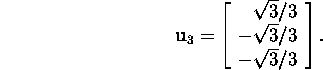
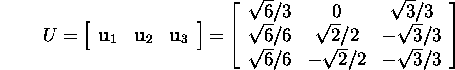
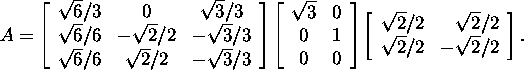
IV Leiame singulaarmaatriksi

mille peadiagonaalil on ruutjuured maatriksi A^TA omaväärtustest (kahanevas järjestuses) ja ülejäänud maatriksi elemendid on nullid.

V Leiame valemite (9) abil maatriksi kaks esimest veeruvektorit,

ja

VI Vektori arvutamiseks leiame Gram-Schmidt'i protsessiga algul vektori , mis on risti vektoritega ja :

Normeerides vektori saame

Seega

ja maatriksi A singulaarlahutuseks on:

Näide 3.3.2. Leiame maatriksi singulaarlahutuse.

I Leiame maatriksi A^TA omaväärtused:

II Leiame maatriksi A^TA nullist erinevate omaväärtuste arvu: r=1.

III Leiame maatriksi A^TA omavektorid:



Kuna omaväärtus 0 on kordne, siis vektori leidmiseks on kasutatud Gram-Schmidt'i ortogonaliseerimisprotsessi. ''Kleebime'' kokku ortogonaalmaatriksi V:

IV Koostame singulaarmaatriksi:

V Arvutame valemite (9) abil maatriksi U ainsa veeruvektori:

Seega, maatriksi A singulaarlahutus on

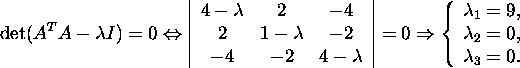
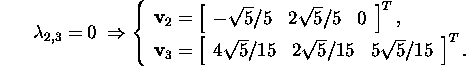
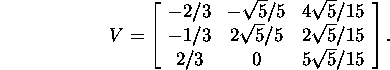
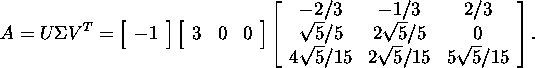
Näide 3.3.3.^* Leiame maatriksi

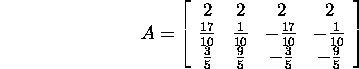
singulaarlahutuse.
Antud -maatriksil A on ülimalt kolm nullist erinevat singulaarväärtust. Järelikult on otstarbekas leida maatriksi A nullist erinevad singulaarväärtused -maatriksi AA ^T abil (mitte -maatriksi A^TA abil). Kuna

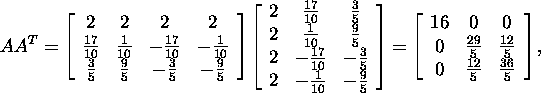
siis maatriksi AA^T karakteristlik võrrand on

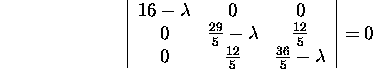
ehk

ja selle võrrandi lahendeiks on ning Kuna ja maatriksi on -maatriks, siis maatriksi peadiagonaalil on maatriksi A singulaarväärtused kahanevas järjekorras ning ülejäänud maatriksi elemendid on n

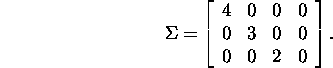
Maatriksi U veeruvektoreiks on maatriksi AA^T ortonormeeritud omavektorid:





Vektorite ja ''kleepimisel'' saame maatriksi

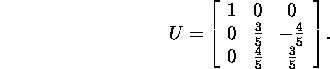
Vastavalt seosele (6) leiame maatriksi V kolm esimest veeruvektorit (maatriksi peadiagonaalil on kolm nullist erinevat elementi) valemi

abil. Seega

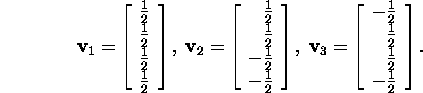
Vektori arvutamiseks leiame Gram-Schmitd'i ortogonaliseerimisprotsessiga algul vektori , mis on risti vektoritega ja :



Kuna siis

ja

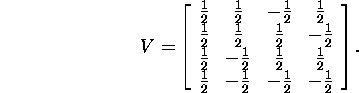
Teostame kontrolli



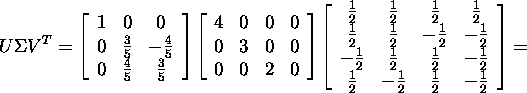
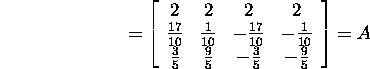
ja

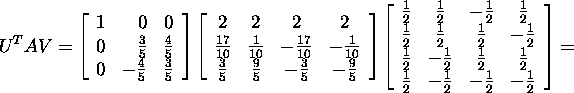
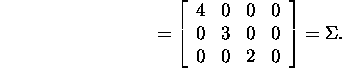
Ülesanne 3.3.1.^* Kasutades näites 3.3.3 saadud maatriksi A singulaarlahutust leida maatriksi A veeruvektorite alamruumi parempoolse nullruumi reavektorite alamruumi ja vasakpoolse nullruumi baasid.

Ülesanne 3.3.2.^* Leida maatriksi 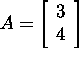singulaarlahutus ja QR-lahutus.

Ülesanne 3.3.3.^* Leida maatriksi singulaarlahutus.