iga nullist erineva vektori
Peatüki
algus: Lineaarsete
algebraliste võrrandisüsteemide lahendamise otsesed meetodid
Eelmine: Maatriksi
LDMT-lahutus ja LDLT-lahutus
Järgmine: Positiivselt
poolmääratud maatriksid
Positiivselt
määratud süsteemid
Definitsioon 6.2.1.
Maatriksit ![]() nimetatakse positiivselt määratuks, kui
nimetatakse positiivselt määratuks, kui
![]()
iga nullist erineva vektori ![]() korral.
korral.
Näide 6.2.1. Maatriks
![]()
on positiivselt määratud, sest ![]() korral
korral
![]()
![]()
Ülesanne 6.2.1.* Näidake,
et maatriks
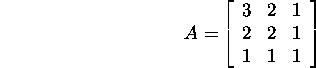
on positiivselt määratud.
Lause 6.2.1. Kui ![]() on positiivselt määratud maatriks ja maatriksi
on positiivselt määratud maatriks ja maatriksi ![]() veeruvektorid on lineaarselt sõltumatud, siis maatriks
veeruvektorid on lineaarselt sõltumatud, siis maatriks
![]()
on samuti positiivselt määratud.
Tõestus. Kui vektori ![]() korral peab paika seos
korral peab paika seos
![]()
siis
![]()
ja maatriksi A positiivsest määratusest järeldub,
et ![]() Kuna maatriksi X veeruvektorid on lineaarselt
sõltumatud, siis tingimusest
Kuna maatriksi X veeruvektorid on lineaarselt
sõltumatud, siis tingimusest ![]() järeldub, et
järeldub, et ![]() Seega, tingimustest
Seega, tingimustest ![]() ja
ja ![]() järeldub, et
järeldub, et ![]() st maatriks B on positiivselt määratud.
st maatriks B on positiivselt määratud. ![]()
Järeldus 6.2.1. Kui
maatriks ![]() on positiivselt määratud, siis
kõik maatriksi A alammaatriksid, mis on saadud maatriksi
A samanumbriliste ridade ja veergude kustutamisel, on positiivselt
määratud ja kõik maatriksi A peadiagonaali elemendid
on positiivsed.
on positiivselt määratud, siis
kõik maatriksi A alammaatriksid, mis on saadud maatriksi
A samanumbriliste ridade ja veergude kustutamisel, on positiivselt
määratud ja kõik maatriksi A peadiagonaali elemendid
on positiivsed.
Tõestus. Kui ![]() on selliste naturaalarvuliste koordinaatidega vektor, et
on selliste naturaalarvuliste koordinaatidega vektor, et
![]()
siis
![]()
on maatriks, mis on saadud ühikmaatriksi In veergudest,
indeksitega ![]() Seega, maatriksi X veeruvektorid on lineaarselt sõltumatud
ja lause 6.2.1 põhjal on maatriks XTAX
positiivselt määratud. Maatriks XTAX on maatriksi
A alammaatriks, mis on saadud maatriksi A ridadest ja veergudest
numbritega
Seega, maatriksi X veeruvektorid on lineaarselt sõltumatud
ja lause 6.2.1 põhjal on maatriks XTAX
positiivselt määratud. Maatriks XTAX on maatriksi
A alammaatriks, mis on saadud maatriksi A ridadest ja veergudest
numbritega ![]() Seega, kõik maatriksi A alammaatriksid, mis on saadud maatriksi
A samanumbriliste ridade j a veergude kustutamisel, on positiivselt
määratud. Valides k=1, saame järelduse väite
teise poole.
Seega, kõik maatriksi A alammaatriksid, mis on saadud maatriksi
A samanumbriliste ridade j a veergude kustutamisel, on positiivselt
määratud. Valides k=1, saame järelduse väite
teise poole. ![]()
Järeldus 6.2.2. Kui
A ![]() on positiivselt määratud, siis maatriksil A leidub lahutus
A=LDMT ja diagonaalmaatriksi
on positiivselt määratud, siis maatriksil A leidub lahutus
A=LDMT ja diagonaalmaatriksi ![]() peadiagonaali
kõik elemendid on positiivsed.
peadiagonaali
kõik elemendid on positiivsed.
Tõestus. Järelduse
6.2.1 põhjal on kõik maatriksi A alammaatriksid
A(1 : k, 1 : k) (1![]() k
k![]() n) positiivselt määratud ja, seega, regulaarsed maatriksid ning
lause 6.1.1 põhjal eksisteerib LDMT-lahutus.
Võttes lauses 6.2.1 X=L-T,
leiame, et maatriks
n) positiivselt määratud ja, seega, regulaarsed maatriksid ning
lause 6.1.1 põhjal eksisteerib LDMT-lahutus.
Võttes lauses 6.2.1 X=L-T,
leiame, et maatriks
![]()
on positiivselt määratud. Kuna
maatriks MTL-T ülemine ühikdiagonaaliga
kolmnurkmaatriks, siis maatriksitel B ja D on sama peadiagonaal
ja seal peavad maatriksi B positiivse määratuse tõttu
olema positiivsed elemendid. ![]()
Lause 6.2.2 (Cholesky
lahutus). Kui maatriks A ![]() on sümmeetriline ja positiivselt määratud, siis leidub täpselt
üks alumine positiivse peadiagonaaliga kolmnurkmaatriks G,
et
on sümmeetriline ja positiivselt määratud, siis leidub täpselt
üks alumine positiivse peadiagonaaliga kolmnurkmaatriks G,
et
![]()
Tõestus. Lause
6.1.2 põhjal leiduvad ja on üheselt määratud
ühikdigonaaliga alumine kolmnurkmaatriks L ja diagonaalmaatriks
![]() nii, et kehtib lahutus (3), so A=LDLT.
Järelduse 6.2.2 kohaselt on maatriksi D
elemendid dk positiivsed. Seetõttu maatriks
nii, et kehtib lahutus (3), so A=LDLT.
Järelduse 6.2.2 kohaselt on maatriksi D
elemendid dk positiivsed. Seetõttu maatriks
![]()
on positiivse peadiagonaaliga alumine kolmnurkmaatriks ja paika peab seos
(5). Lahutuse (5) ühesus järeldub lahutuse (3)
ühesusest. ![]()
Lahutus (5) on tuntud Cholesky lahutuse nime all.
Maatriksit G nimetatakse maatriksi A Cholesky kolmnurkmaatriksiks.
Sümmeetrilise ja positiivselt määratud
maatriksiga A võrrandisüsteemi
![]()
lahendamiseks tuleb, esiteks, leida maatriksi A Cholesky
kolmnurkmaatriksiks G. Teiseks, tuleb lahendada kolmnurkmaatriksiga
süsteem
![]()
Kolmandaks, tuleb lahendada süsteem
![]()
Cholesky lahutust on võimalik leida samm-sammult.
Lause 6.2.3. Kui maatriks
A ![]() on sümmeetriline ja positiivselt määratud,
siis tähistuse
on sümmeetriline ja positiivselt määratud,
siis tähistuse
![]()
korral on maatriks A esitatav kujul
![]()
kusjuures ![]() Maatriks
Maatriks ![]() on positiivselt määratud. Kui
on positiivselt määratud. Kui
![]()
siis A=GGT, kusjuures
![]()
Tõestus. Kontrollime lahutuse (6)
õigsust:
![]()
![]()
![]()
Kui
![]()
siis
![]()
![]()
Kuna maatriks A on positiivselt määratud ja maatriksi
X veeruvektorite süsteem on lineaarselt sõltumatu, siis
lause 6.2.1 põhjal on positiivselt määratud
ka maatriks
![]()
ja järelduse 6.2.1 väitel on maatriks
![]() samuti positiivselt määratud ning võime analoogiliselt
maatriksi A lahutusega blokkideks jaotada ka maatriks
samuti positiivselt määratud ning võime analoogiliselt
maatriksi A lahutusega blokkideks jaotada ka maatriks ![]() blokkideks, jne.
blokkideks, jne.
Näide 6.2.1. Leiame maatriksi
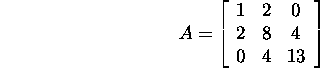
LU-lahutuse, LDMT-lahutuse,
LDLT-lahutuse
ja Cholesky lahutuse.
Nendime, et kui maatriksi A peamiinorid on nullist
erinevad, siis maatriksi A viimisel Gaussi
teisenduse abil kolmnurkkujule, leiame samaaegselt nii maatriksi L
kui ka maatriksi U. Nimelt, alumise kolmnurkmaatriksi L element
lij ![]() võrdub teguriga, millega tuleb j-ndat rida korrutada mahalahutamisel
i-ndast reast i-ndas reas oleva elemendi nullistamisel. Leiame,
et
võrdub teguriga, millega tuleb j-ndat rida korrutada mahalahutamisel
i-ndast reast i-ndas reas oleva elemendi nullistamisel. Leiame,
et
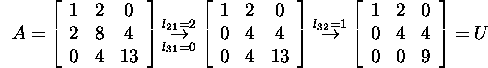
ja
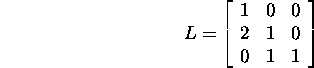
ning
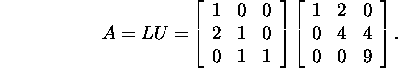
Teades maatriksi A jaoks LU-lahutust,
leiame maatriksi A jaoks LDMT-lahutuse,
LDLT-lahutuse
ja Cholesky lahutuse:
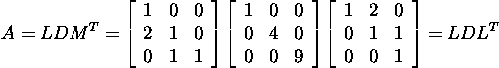
ja
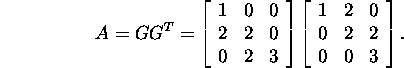
Leiame maatriksi A Cholesky lahutuse ka samm-sammult, kasutades
lauses 6.2.3 esitatud algoritmi. Kuna esimesel sammul
![]()
siis
![]()
Järgneval sammul
![]()
ja
![]()
Seega
![]()
ja
![]()
ning
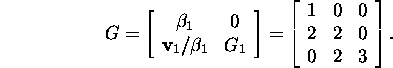
Ülesanne 6.2.2.* Leidke
positiivselt määratud maatriksi
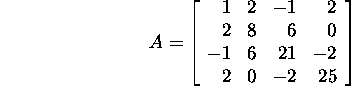
Cholesky lahutus.
Ülesanne 6.2.3.* Lahendage
võrrandisüsteem ![]() kus
kus
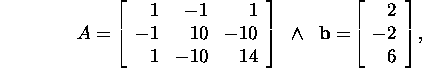
kui on teada maatriksi A Cholesky lahutus
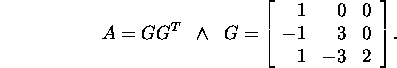
Peatüki
algus: Lineaarsete
algebraliste võrrandisüsteemide lahendamise otsesed meetodid
Eelmine: Maatriksi
LDMT-lahutus ja LDLT-
Järgmine: Positiivselt
poolmääratud maatriksid