Peatüki
algus: Maatriksid
Eelmine: Maatriksi
omaväärtused ja omavektorid
Järgmine: Maatriksi normid
ja konditsiooniarvud
Maatriksi ![]() omavektor
omavektor ![]() määrab ruumis
määrab ruumis ![]() ühemõõtmelise
alamruumi, mis on invariantne
maatriksiga A vasakult korrutamise suhtes.
ühemõõtmelise
alamruumi, mis on invariantne
maatriksiga A vasakult korrutamise suhtes.
Definitsioon 2.6.1.
Alamruumi ![]() nimetatakse invariantseks maatriksiga A (vasakult) korrutamise
suhtes, kui
nimetatakse invariantseks maatriksiga A (vasakult) korrutamise
suhtes, kui ![]()
Lause 2.6.1. Kui ![]() ja AX=XB, siis maatriksi X veeruvektorite ruum
ja AX=XB, siis maatriksi X veeruvektorite ruum ![]() on invariantne maatriksiga A vasakult
korrutamise suhtes ja reavektorite ruum
on invariantne maatriksiga A vasakult
korrutamise suhtes ja reavektorite ruum ![]() on invariantne maatriksiga B paremalt korrutamise suhtes. Lisaks,
kehtivad seosed
on invariantne maatriksiga B paremalt korrutamise suhtes. Lisaks,
kehtivad seosed
![]()
ja
![]()
Tõestus. Kui ![]() siis
siis
![]()
ja
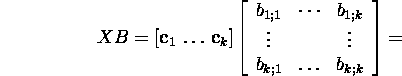
![]()
ning
![]()
Seega, maatriksi X veeruvektorite ruum ![]() on invariantne maatriksiga A vasakult
korrutamise suhtes. Analoogiliselt tõestatakse, et reavektorite
ruum
on invariantne maatriksiga A vasakult
korrutamise suhtes. Analoogiliselt tõestatakse, et reavektorite
ruum ![]() on invariantne maatriksiga B paremalt korrutamise suhtes. Kui
on invariantne maatriksiga B paremalt korrutamise suhtes. Kui ![]() siis
siis
![]()
st ![]() on maatriksi A omaväärtus,
kui
on maatriksi A omaväärtus,
kui ![]() on maatriksi B omaväärtus. Nendime, et
on maatriksi B omaväärtus. Nendime, et
![]()
Järelikult, kui maatriksi X veeruvektorid on lineaarselt
sõltumatud, siis ![]() Kui
Kui ![]() ja X on regulaarne ruutmaatriks
ja X on regulaarne ruutmaatriks ![]() ,
siis seosest AX=XB järeldub, et A=XBX-1
ning
,
siis seosest AX=XB järeldub, et A=XBX-1
ning
![]()
st maatriksi A iga omaväärtus
on maatriksi B omaväärtus, ![]() ja seega
ja seega ![]()
Definitsioon 2.6.2.
Maatrikseid ![]() nimetatakse sarnasteks, kui leidub selline regulaarne maatriks
nimetatakse sarnasteks, kui leidub selline regulaarne maatriks ![]() et A=XBX-1.
et A=XBX-1.
Lause 2.6.1 viimase väite
põhjal on sarnaste maatriksite spektrid
võrdsed. See väide järeldub ka vahetult, sest
![]()
![]()
Ülesanne 2.6.1.* Kas maatriksid
A ja B on sarnased, kui
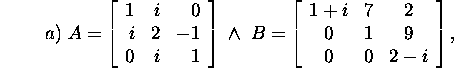
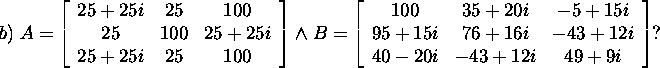
Tõestus. Kui ![]() st
st![]()
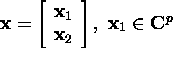 ja
ja ![]() siis
siis
![]()
Kui ![]() siis
siis
![]()
Kui ![]() siis
siis
![]()
Järelikult,
![]()
Kuna hulkade ![]() ja
ja ![]() võimsused on samad, siis peab paika lause väide.
võimsused on samad, siis peab paika lause väide.
Näide 2.6.1. Leiame lause
2.6.2 abil maatriksi
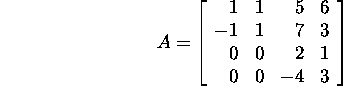
spektri. Selleks leiame maatriksite 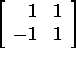 ja
ja 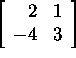 omaväärtused:
omaväärtused:
![]()
![]()
Seega maatriksi spektrks on ![]()
Ülesanne 2.6.2.* Leidke lause 2.6.2 abil maatriksi A spekter , kui
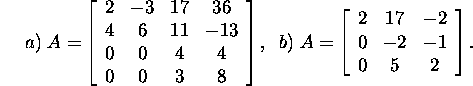
Definitsioon 2.6.3. Maatriksit
![]() nimetatakse unitaarmaatriksiks, kui QHQ=QQH=I.
nimetatakse unitaarmaatriksiks, kui QHQ=QQH=I.
Ülesanne2.6.3.* Kas maatriks
Q on unitaarmaatriks, kui
![]()
![]()
Lause 2.6.3 (teoreem
maatriksi QR-lahutusest). Kui ![]() ,
siis maatriks A on esitatav kujul A=QR, kus maatriks
,
siis maatriks A on esitatav kujul A=QR, kus maatriks
![]() on unitaarmaatriks ja R
on unitaarmaatriks ja R ![]() on ülemine kolmnurkne maatriks.
on ülemine kolmnurkne maatriks.
Lause 2.6.4. Kui ![]()
![]()
ja rank(X)=p, siis leidub selline unitaarmaatriks
![]() et
et
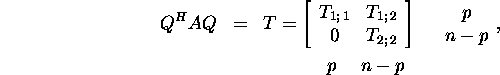
kus ![]()
Tõestus. Vaatleme maatriksi ![]() korral
selle QR-lahutust
korral
selle QR-lahutust 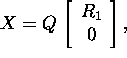 kus
kus ![]() ja
ja ![]() Paigutades selle maatriksi X esituse seosesse (20), saame
Paigutades selle maatriksi X esituse seosesse (20), saame
![]()
Maatriksi QHAQ spekter
ühtib maatriksi A spektriga, st ![]() Esitades maatriksi A kujul
Esitades maatriksi A kujul
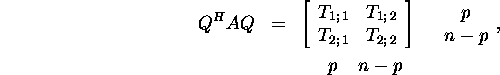
leiame, et
![]()
![]()
Seega lause väide peab paika.
Märkus 2.6.1. Lause 2.6.4 võimaldab, teades maatriksi mingit invariantset alamruumi, teisendada maatriksi unitaarse sarnasusteisenduse abil kolmnurksele blokk-kujule.
Lause 2.6.5 (Schuri
lahutus). Kui ![]() siis leidub selline unitaarne maatriks
siis leidub selline unitaarne maatriks ![]() et
et
![]()
kusjuures ![]() ja
ja ![]() on rangelt ülemine kolmnurkmaatriks, st ülemine kolmnurkmaatriks,
mille peadiagonaalil on nullid. Maatriksit Q võib valida
selliselt, et maatriksi A omaväärtused on D peadiagonaalil
etteantud järjekorras.
on rangelt ülemine kolmnurkmaatriks, st ülemine kolmnurkmaatriks,
mille peadiagonaalil on nullid. Maatriksit Q võib valida
selliselt, et maatriksi A omaväärtused on D peadiagonaalil
etteantud järjekorras.
Tõestuseks kasutame matemaatilist induktsiooni.
Kuna väide peab paika n=1 korral, siis induktsiooni baas on
olemas. Näitame induktsiooni sammu lubatavust. Eeldame, et väide
peab paika maatriksite korral, mille järk on väiksem-võrdne
kui ![]() Näitame, et see väide peab siis paika ka järgu k
korral. Kui
Näitame, et see väide peab siis paika ka järgu k
korral. Kui ![]() ja
ja ![]() siis lemma 2.6.4 põhjal, valides
siis lemma 2.6.4 põhjal, valides ![]() , leidub selline unitaarmaatriks U,
et
, leidub selline unitaarmaatriks U,
et
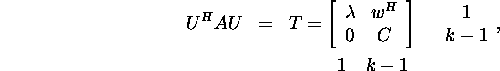
Kuna maatriks C ![]() selle maatriksi korral peab paika lause väide, st leidub selline unitaarmaatriks
selle maatriksi korral peab paika lause väide, st leidub selline unitaarmaatriks
![]() et
et ![]() on ülemine kolmnurkmaatriks. Kui
on ülemine kolmnurkmaatriks. Kui ![]() siis
siis
![]()
![]()
![]()
ja seega on maatriks QHAQ ülemine kolmnurkmaatriks.
Näide 2.6.2. Olgu
![]()
Näitame, et Q on unitaarmaatriks.
Leiame korrutise QHAQ.
Kontrollime maatriksi Q on unitaarsust:
![]()
![]()
Leiame korrutise
![]()
![]()
Järelikult, oleme saanud maatriksi A Schuri
lahutuse.
Seos (21) on esitatav kujul AQ=QT.
Asendades ![]() kus vektoreid
kus vektoreid ![]() nimeta takse Schuri vektoreiks, viimasesse võrdusesse, saame
nimeta takse Schuri vektoreiks, viimasesse võrdusesse, saame
![]()
ehk
![]()
![]()
või
![]()
Sellest seosest järeldub, et alamruumid ![]() (k=1:n)
on invariantsed maatriksiga A vasakult korrutamise suhtes ja Schuri
vektor
(k=1:n)
on invariantsed maatriksiga A vasakult korrutamise suhtes ja Schuri
vektor ![]() on maatriksi A omavektoriks
parajasti siis, kui maatriksi
on maatriksi A omavektoriks
parajasti siis, kui maatriksi ![]() -ndas
veerus on vaid nullid.
-ndas
veerus on vaid nullid.
Definitsioon 2.6.4. Kui
![]() ja AHA=AAH, siis maatriksit A
nimetatakse normaalmaatriksiks.
ja AHA=AAH, siis maatriksit A
nimetatakse normaalmaatriksiks.
Ülesanne 2.6.4.* Kas maatriks
A on normaalmaatriks, kui
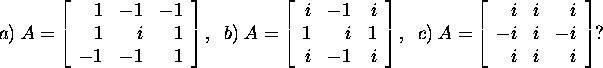
Lause 2.6.6. Maatriks ![]() on normaalmaatriks parajasti siis, kui leidub
selline unitaarmaatriks
on normaalmaatriks parajasti siis, kui leidub
selline unitaarmaatriks ![]() et
et ![]()
Tõestus. Kui maatriks A on unitaarselt
sarnane diagonaalmaatriksiga D, siis
![]()
![]()
ja kuna diagonaalmaatriksid on kommuteeruvad, siis AHA=AAH
ja maatriks A on normaalmaatriks.
Vastupidi, kui maatriksi A on normaalmaatriks ja selle maatriksi
Schuri lahutuseks on QHAQ=T, siis ka T
on normaalmaatriks, sest
![]()
ja
![]()
Kuna kolmnurkmaatriks on normaalmaatriks vaid siis, kui see maatriks on
diagonaalmaatriks, siis on tõestatud, et unitaarmaatriks
on sarnane diagonaalmaatriksiga.
Lause 2.6.7 (blokk-diagonaal-lahutus). Olgu
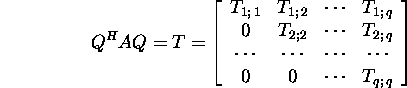
on maatriksi ![]() Schuri lahutus, kusjuures blokid
Schuri lahutus, kusjuures blokid ![]() on ruutmaatriksid. Kui
on ruutmaatriksid. Kui ![]() siis eksisteerib selline regulaarne maaatriks
siis eksisteerib selline regulaarne maaatriks ![]()
![]() et
et
![]()
Järeldus 2.6.1. Kui ![]() siis leidub selline regulaarmaatriks X, et
siis leidub selline regulaarmaatriks X, et
![]()
kusjuures ![]() ja
ja ![]() ning iga
ning iga ![]() on rangelt ülemine kolmnurkmaatriks.
on rangelt ülemine kolmnurkmaatriks.
Lause 2.6.8 (Jordani
lahutus). Kui ![]() siis leidub selline regulaarne
siis leidub selline regulaarne ![]() et
et ![]() kusjuures
kusjuures ![]() ja
ja
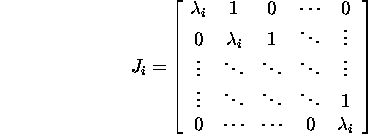
on ![]() Jordani blokk ning maatriks J kannab maatriksi A Jordani
normaalkuju nime.
Jordani blokk ning maatriks J kannab maatriksi A Jordani
normaalkuju nime.
Tõestus. Vaadake Lankaster (1982, lk 143).
Näide 2.6.3. Leiame, kasutades paketti ''Maple'',
kahe maatriksi Jordani lahutuse A=XJX-1:
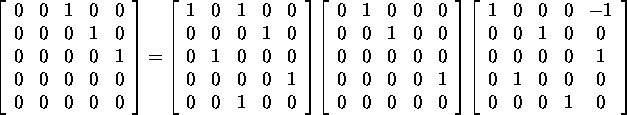
Peatüki
algus: Maatriksid
Eelmine: Maatriksi
omaväärtused ja omavektorid
Järgmine: Maatriksi normid
ja konditsiooniarvud