Peatüki algus: Singulaarlahutus
Eelmine: Singulaarlahutuse olemasolu
Järgmine: Singulaarlahutuse algoritm

Seosest (2) järelduvad seosed
 
ja
 

Lause 3.2.1. Kui   ja   siis iga  = korral peavad paika seosed
 

ja

ning

Tõestus. Olgu n>m. Vaatleme seost (3), mis on esitatav kujul

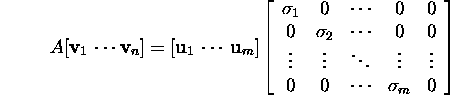
ehk

mis maatriksi esimeses m veerus paiknevate elementide jaoks ongi seos (5). Vaatleme seost (4), mis on esitatav kujul

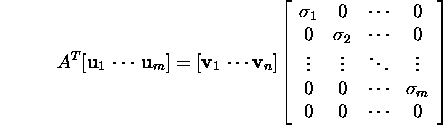
ehk

mis elemenditi kujutab seost (6). Rõhutame, et lause tõestuses on sümboliga ''0'' tähistatud ka teatud nullidest koosnevad blokid. 

Lause 3.2.2. Kui maatriksi  singulaarlahutuses (2) esinevad singulaarväärtused rahuldavad võrratusi

siis

• 
• 
• 
• 
• rank(A)=r;
• maatriksi A singulaarväärtused on võrdsed hüperellipsoidi


pooltelgede pikkustega;

• 

Tõestame esimese neist omadustest. Vaatleme seost . Kuna

siis

ehk

Seega

Lause 3.2.3. Kui  ja  on maatriksi A singulaarlahutus, siis  veeruvektorid on AA^T normeeritud omavektorid ja  veeruvektorid on A^TA normeeritud omavektorid. Maatriksi A singulaarväärtused avalduvad ruutjuurtena nii A^TA kui ka AA^T omaväärtustest.

Tõestus. Lähtudes maatriksi A singulaarlahutusest leiame maatriksite AA^T ja A^TA esitused:
 

 
ja
 
Kuna maatriksid  ja  on diagonaalmaatriksid, siis ortogonaalmaatriksid U ja V peavad esitustes (7) ja (8) koosnema vastavalt maatriksi AA^T ja A^TA omavektoreist.