Determinants

Let us consider an matrix, the so-called matrix of order n

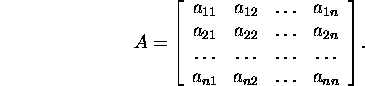
Definition 2.3.1. Arbitrary ordering of indeces is called a permutation.

Definition 2.3.2. The ordering of two indeces in the permutation is called natural if the smaller index stands before the greatest one; in the opposite case, the greater index standing before the smaller one, it is said that the two indeces form an inversion.

Definition 2.3.3. A determinant is a law (mapping, function) that associates with each square matrix A a number, so-called determinant of the matrix

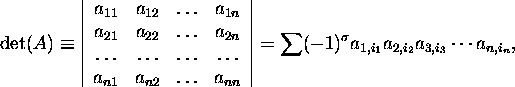
where the summation goes over all the permutations of indeces and is the number of inversions in the permutation of the row indeces. We will use expressions: determinant of order n and its rows and cocumns.

Example 2.3.1. Let us consider the third order determinant





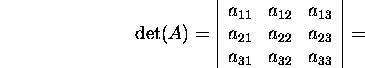
Let us examine the last summand (-1)³a₁₃a₂₂a₃₁. In the permutation 3 2 1 of the column indeces the index 3 forms with the index 2 and the index 1 an inversion. The index 2 does the same with the index 1. So the number of inversions in the permutation of the column indices is equal to 3.

Problem 2.3.1.^* Which sign has the product

of elements of determinant expression.

Properties of determinant

• The determinants of a matrix and its transpose are equal,
• Multiplying all the elements of the row (column) of the determinant by the same number the determinant will be multiplied by the same number.
• Interchanging two rows (columns) of the determinant the determinant will change its sign.
• If two rows (columns) of the determinant are identical, then the determinant is equal to 0.
• If each element in the row (column) of the determinant is a sum of two summands, then the determinant expands into the sum of two determinants, where in the considered row (column) in the first of them there will be the first summands and in the second of them there will be the second summands, and all the remaining rows (columns) will be identical to those of the given matrix:
  
  
• The determinant will not change if add to the row (column) an arbitrary row (column) multiplied by an arbitrary number.
• The fundamental formulas of the determinants theory (or theorem of expansion by cofactors) are valid:
  
  
  
  where
  
  is the Kronecker symbol and A_ik is the product of the number (-1)^i+k and the determinant of the matrix got of the given matrix by deleting the i-th row and k-th column.

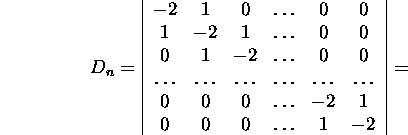
Example 2.3.2. Let us evaluate the determinant of order n, using the expansion by cofactors by the first column and then by the first row.





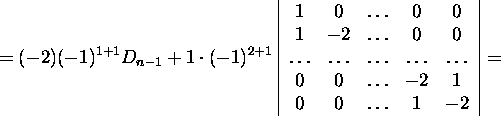
or
 
Equation (1) is a linear homogeneous difference equation with constant coefficients which has the solution of type Let us try to find them:

We are interested in non-trivial solution. So we have get a quadratic equation

to find the solution of the difference equation (1). It has the solutions , and so one of the solutions of equation (1) is D_n=(-1)ⁿ. As the number -1 is a double solution of the quadratic equation, D_n=(-1)ⁿn will be a solution of the equation (1), too. Thus, we have got two linearly independent particular solutions of the linear homogeneous difference equation with constant coefficients. The general solution of the equation can be expressed in form

From the conditions D₁=-2 and D₂=3 we can find the coefficients C₁ and C₂:

So the given problem has the solution

Problem 2.3.2.^* Compute the determinant of order n

Example 2.3.3. Evaluate the Vandermonde determinant

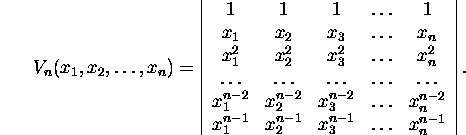
We substract x₁ times the penultimate row from the last row, then x₁ times the (n-2)-th row from the penultimate row, then x₁ times (n-3)-th row from the (n-2)-th row etc., in the end x₁ times the second row from the first one. As a result, we get

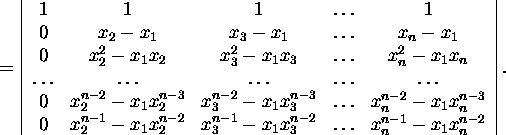
Using the expression by the first column and factoring out the common factors in the elements, we get

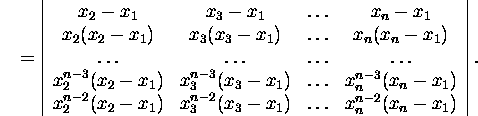
Factoring out from the first columns the common factor x₂-x₁, from the second column , from the (n-1)-th column x_n-x₁, we get

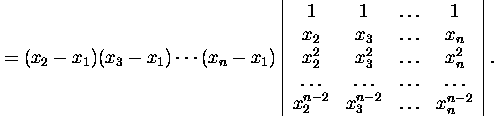
Using the same operations cycles, we shall result in

Proposition 2.3.1 (The Laplace expansion theorem). It holds the so-called Laplace formula

where the summation on the right goes over all determinants (minors) M_k of order k that can be formed of rows i₁, i₂, , i_k and columns j₁, j₂, , j_k, and A_n-k is the product of the number and the determinant of the matrix remaining from the matrix A by deleting the rows i₁, i₂, , i_k and the columns j₁, j₂, , j_k used ny forming the minor M_k.

Proof. See Kangro (1962, pp. 37-39).

Example 2.3.4. Using the Laplace expansion by two first rows, transform the determinant

As only three minors not equal to zero can be formed the two first rows, we get the expansion

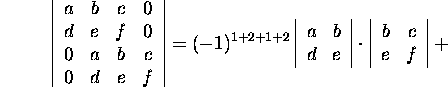
Problem 2.3.3.^* Compute by the use of the Laplace formula the determinant

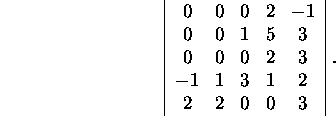
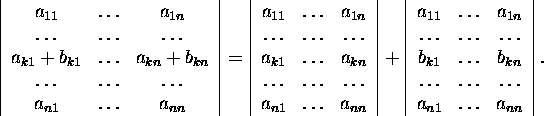
By the Laplace expansion theorem, it holds for each matrix the equality
 

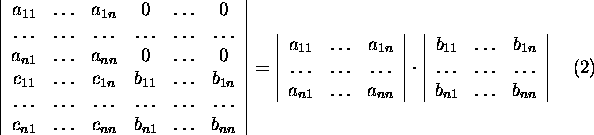
Choosing 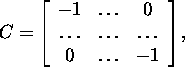we transform the determinant

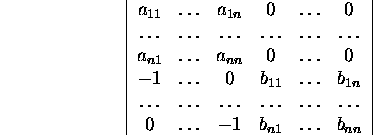
so that all the elements b_ij become zeros. To make into zeros we have to add to the (n+1)-th column b₁₁ times the elements of the first column, b₂₁ times the elements of the second column etc, and, in the end, b_n1 times the elements of the n-th column. Next we make into zeros the elements For this we add to the (n+2)-th column b₁₂ times the first column, b₂₂ times the second column etc, and, in the end, b_n2 times the n-th column etc. The last step will nullity the elements For this we add to the 2n-th column b_1n times the first column, b_2n times the second column etc, and, in the end, b_nn times the n-th column. The result will be





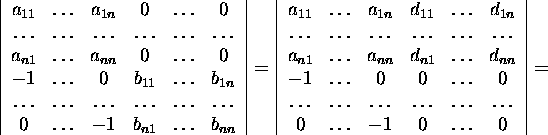
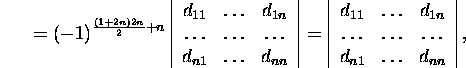
where
 
Taking into account (2) and the fact that, by (3), , we reach the assertion.

Proposition 2.3.1 (the theorem about the determinant of the product of matrices). For arbitrary matrices A and B of order n it holds