Cayley-Hamilton Theorem

Proposition 2.8.1 (Cayley-Hamilton theorem). If and

then p(A)=0, i.e., the matrix A satisfies its characteristic equation.

Proof. According to proposition 2.6.7, there exists a regular matrix such that

where

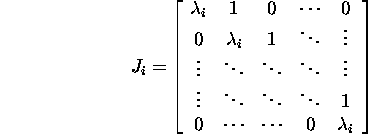
is an upper bidiagonal matrix (Jordan block) that has on its main diagonal the eigenvalue of the matrix A( at least m_i-mutiple eigenvalue of the matrix A since to this eigenvalue may correspond some more Jordan's blocks) and Since then and )^m_i=0. If is the characteristic polynomial of the matrix A and the zeros of this polynomial are , then

and

We show that p(J)=0. Let the matrix J have the block form:

We obtain that















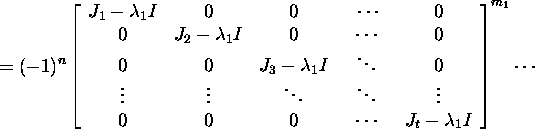
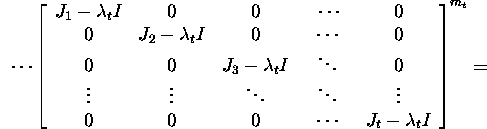
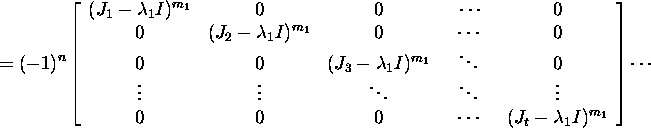
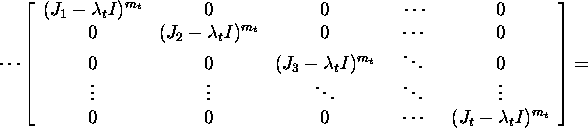
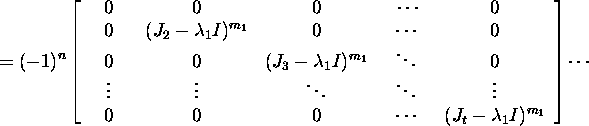
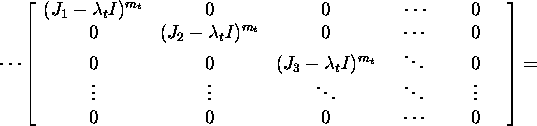
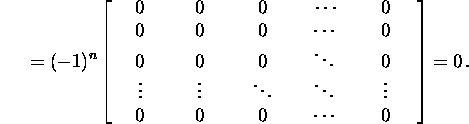
From the relation X^-1AX=J it follows that A=XJX^-1. We complete the proof with

Example 2.8.1. Verify the assertion of the Cayley-Hamilton theorem for the matrix

.

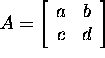We construct the characteristic polynomial

and find

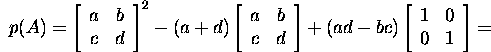
Exercise 2.8.1.* Let

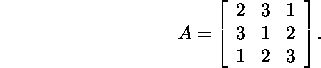
Compute A², and using the Cayley-Hamilton theorem, find the matrix

Definition 2.8.1. A polynomial is called a nullifying polynomial of the matrix if q(A)=0.

The characteristic polynomial of the matrix is a nullifying polynomial of this matrix (by the Cayley-Hamilton theorem).

Definition 2.8.2. The nullifying polynomial of the matrix of the lowest degree is called the minimal polynomial of the matrix A.

Exercise 2.8.1. Verify that the characteristic polynomial of matrix is divisible by the minimal polynomial of the matrix A without remainder.

Proposition 2.8.2. Let and be the characteristic polynomial and the minimal polynomial of the matrix A, respectively. Let the greatest common divisor of the matrix that is, the matrix of algebraic complements of the elements of the matrix -A) , be . Then,

Proof. See Lankaster (1982, p. 123-124).

Example 2.8.2. Find the characteristic polynomial and the minimal polynomial of the matrix D=diag(a,a,b,b). First we find that





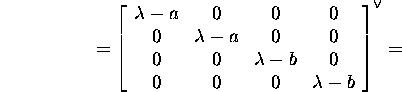
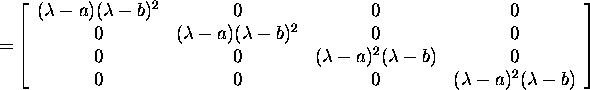
and the greatest common divisor of the elements of the matrix is By the assertion of proposition 2.8.2 Let us check



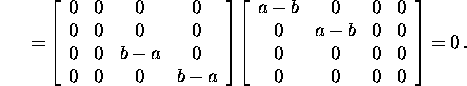
Indeed, is the nullifying polynomial. It is easy to verify that no polynomial of first degree can nullify the matrix A. Thus, is the minimal polynomial of the matrix A.

Example 2.8.3. Find the characteristic and the minimal polynomials of the matrices

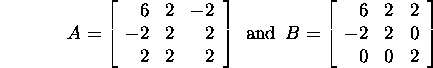
First we find the characteristic polynomials

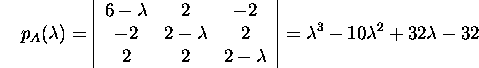
and

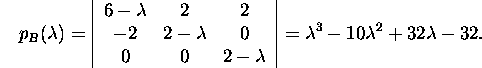
Next we find the minimal polynomials:

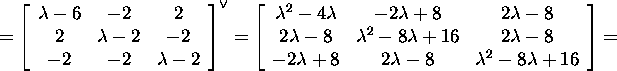
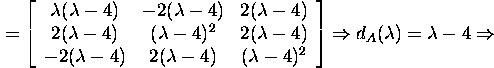
and
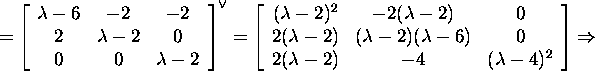