Norm of a Vector

Definition 1.5.1. A vector space (over the number field ) is called a normed space, if to each vector there corresponds a certain non-negative real number called the norm of the vector, such that the following conditions are satisfied:

1. identity axiom);

2. (ogencity axiom);

3. (triangle inequality).

Definition 1.5.2. The distance between two vectors in the normed space is defined by the formula

Proposition 1.5.1 (Hölder inequality). If

then

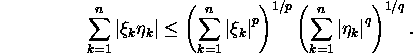
Proof. See E.Oja, P.Oja (1991, pp. 11-12).

Proposition 1.5.2 (Minkowski inequality). If

then

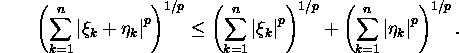
Proof. See E.Oja, P.Oja (1991, pp. 10-11).

Example 1.5.1. One defines in the p-norm of the vector by the formulas



Let us verify that the p-norm satisfies the conditions 1-3 in definition 1.5.1:

;

using the Minkowski inequality, we get

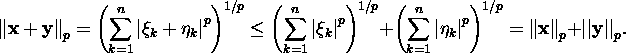
Verify conditions 1-3 in case of the norm !
The most often used p-norms are:

Problem 1.5.1.^* Let be given the vectors ja Find

Proposition 1.5.3. All the p-norms of the space are equivalent, i.e., if and are the p-norms of the space , then there exist positive constants c₁ and such that

At the same time

Let us prove the last three assertions:



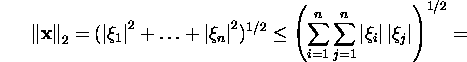
Using the Hölderi inequality, we get in case p=q=2 that

Proposition 1.5.4. A space with scalar product is a normed space with the norm

Proof. Let us verify the validity of conditions 1-3:











is the notation for the real part of the complex number

Proposition 1.5.5. In the normed space with scalar product it holds the parallelogram rule:

Proof. By the immediate check, we get

Definition 1.5.3. It is said that the sequence of the elements of the space converges with respect to the p-norm to the element if

In this case we shall write

Remark 1.5.1. Since all the p-norms of the space are equivalent, this implies that the convergence of the sequence with respect to the -norm will yield its convergence with respect to the -norm.

Problem 1.5.2. Show that if , then

Problem 1.5.3. Show that if , then

where and , . Find such a constant c_n, that

Definition 1.5.4. A vector is called an approximation to the vector if it differs little from in some sense.

Definition 1.5.5. In case of the fixed norm , the quantity

is called the absolute error of the approximation to the vector and the quantity

is called the relative error of the approximation ().

In case of the norm the relative error can be considered as an index of the correct significant digits. Namely, if then the greatest component of the vector has k correct significant digits.

Example 1.5.2. Let and Find and , and then the number of the correct significant digits of the greatest component of the approximation by . We get ja and Thus the greatest component of has three correct significant digits. At the same time, the component has only one correct significant digit.