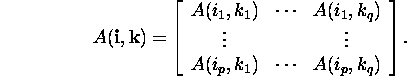The vector space of all 
matrices
with real elements will be denoted by 
and
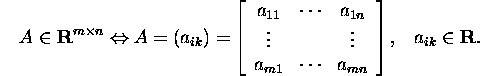
The element of the matrix A that stands in the i-th row and
k-th column will be denoted by aik or A(i,k)
or [A]ik. The main operations with matrices are
following:
Problem 2.1.1.* Let
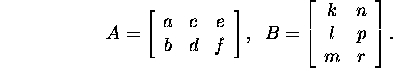
Find the matrix AB.
Problem 2.1.2.* Let
Find the matrix An-1.
Problem 2.1.3.* Let
Prove that
Example 2.1.1.* Let us show that
multiplication of matrices is not commutative.
Let
We find the products:
As 
does not hold for the example, multiplication of matrices is not commutative
in general.
Proposition 2.1.1. If 
and 
then
Proof. If C=(AB)T,
then
If D=BTAT, we also have
Definition
2.1.1. A matrix 
is called symmetric if AT=A and skew-symmetric
if AT=-A.
Problem 2.1.4.* Is matrix A symmetric
matrix or skew-symmetric matrix if
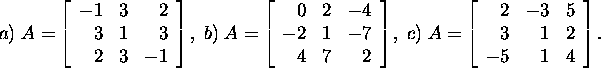
Proposition 2.1.2. Each matrix
can be expressed as a sum of a symmetric matrix
and a skew-symmetric matrix.
Proof. Each matrix
can be expressed as A=B+C, where B=(A+AT)/2
and C=(A-AT)/2. As
and
the proposition holds. 
Problem 2.1.5.* Represent the matrix
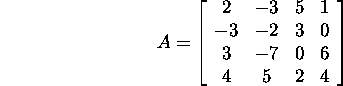
as a sum of a symmetric and a skew-symmetric
matrix.
Definition
2.1.2. If A is a matrix
with complex elemtnts, i.e., 
then the transposed scew-symmetric matrix AH will
be defined by the equality
Definition 2.1.3. A
matrix 
is called an Hermitian matrix if
Problem 2.1.6.* Is matrix A an
Hermitian matrix if
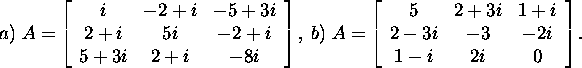
Problem 2.1.7.* Let 
Show that matrices AAH and AHA are
Hermitian matrices.
The matrix 
can be expressed both by the column-vectors 
k
= 1 : n) of the matrix A and by the row-vectors 
( i = 1 : m ) of the transpose of matrix A ("pasting'' the
matrices of the column-vectors or of the transposed row-vectors)
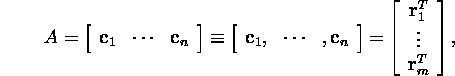
where 
and 
and
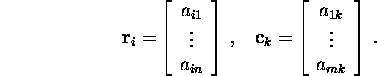
Example 2.1.2. Let us demonstrate these notions
on a matrix 
:
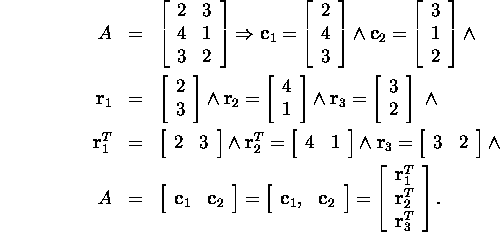
If 
then A(i,:) denotes the i-th row of the matrix A,
i.e.,
and 
denotes the k-th column of the matrix A, i.e.,
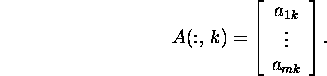
If 
then
and if 
then
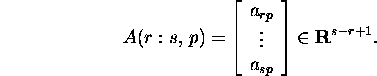
If 
and 
and 
where
then the corresponding submatrix is
and 
then 