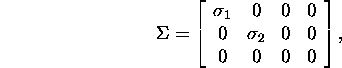
kus
optimaalse lahendi. Vektori
st
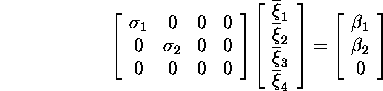
ehk
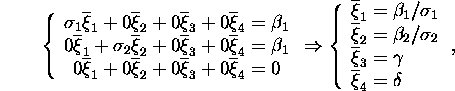
kus
Nendime, et saadud
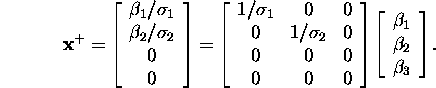
Antud näiteülesande optimaalne lahend
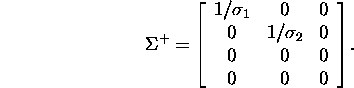
Maatriks
Peatüki
algus: Pseudo-pöördmaatriks
Eelmine: Vähimruutude meetod
Järgmine: Maatriksi Jordani
kuju
Uurime järgnevalt optimaalse lahendi leidmise algoritmi.
Näide 4.2.1. Olgu ![]() ja
ja
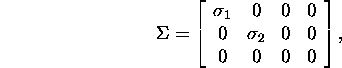
kus ![]() ja
ja ![]() Leiame süsteemi
Leiame süsteemi
![]()
optimaalse lahendi. Vektori ![]() ristprojektsioon ruumile
ristprojektsioon ruumile ![]() on
on ![]() ja
ja ![]() Lahendi
Lahendi ![]() saamiseks tuleb la hendada süsteem
saamiseks tuleb la hendada süsteem
![]()
st
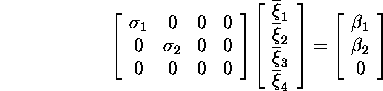
ehk
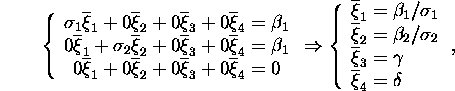
kus ![]() on suvalised. Valides
on suvalised. Valides ![]() saame minimaalse 2-normiga lahendi
saame minimaalse 2-normiga lahendi
![]()
Nendime, et saadud ![]() avaldub ka kujul
avaldub ka kujul
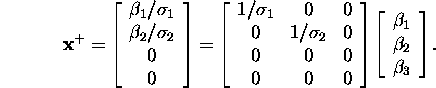
Antud näiteülesande optimaalne lahend ![]() on saadav vabaliikmete vektorist
on saadav vabaliikmete vektorist ![]() selle korrutamisel vasakult maatriksiga
selle korrutamisel vasakult maatriksiga
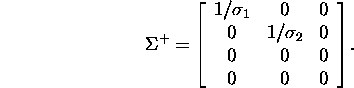
Maatriks ![]() on saadav maatriksist
on saadav maatriksist ![]() selle transponeerimisel ja seejärel nullist erinevate elementide asendamisel
nende pöördelementidega. Seega,
selle transponeerimisel ja seejärel nullist erinevate elementide asendamisel
nende pöördelementidega. Seega, ![]()
Üldistame näites 4.2.1. saadud tulemuse
![]()
siis võrrandisüsteemi
![]()
optimaalne lahend ![]() avaldub kujul
avaldub kujul
![]()
kus
![]()
Definitsioon 4.2.1.
Olgu
![]()
maatriksi ![]() singulaarlahutus. Maatriksi A pseudo-pöördmaatriksiks
nimetatakse maatriksit
singulaarlahutus. Maatriksi A pseudo-pöördmaatriksiks
nimetatakse maatriksit
![]()
kus ![]() ja
ja ![]() on määratud seostega (1-3).
on määratud seostega (1-3).
Ülesanne 4.2.1. Olgu ![]() ja
ja ![]() Näidake, et A+=A-1.
Näidake, et A+=A-1.
Näide 4.2.2. Leiame
näites 3.3.2 esitatud
maatriksi ![]() pseudo-pöördmaatriksi. Selles
näites leidsime maatriksi A singulaarlahutuse
pseudo-pöördmaatriksi. Selles
näites leidsime maatriksi A singulaarlahutuse
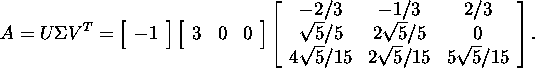
Definitsiooni 4.2.1 põhjal
![]()
so
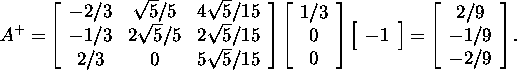
Lause 4.2.2. Kui ![]() siis süsteemi
siis süsteemi ![]() optimaalne lahend
optimaalne lahend
(vähimruutude mõttes)
![]() on leitav valemiga
on leitav valemiga
![]()
Tõestus. Vektori korrutamisel ortogonaalmaatriksiga
UT säilib vektori 2-norm.
Järelikult,
![]()
Teostame asenduse, ![]() Seega
Seega
![]()
Lause 4.2.1 põhjal on avaldist ![]() minimiseerivaks vektoriks
minimiseerivaks vektoriks
![]()
ja vektor
![]()
minimiseerib avaldise ![]()
Näide 4.2.3. Leiame süsteemi
![]()
optimaalse lahendi. Näites 4.2.2 leidsime süsteemimaatriksi
![]()
pseudopöördmaatriksi
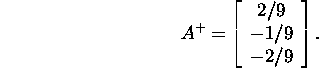
Lause 4.2.2 põhjal saame optimaalse lahendi
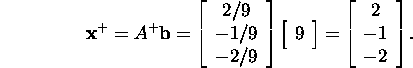
Näide 4.2.4. Leiame süsteemi
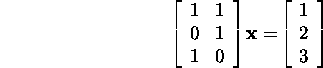
optimaalse lahendi. Näites
3.3.1 leidsime süsteemimaatriksi A singulaarlahutuse
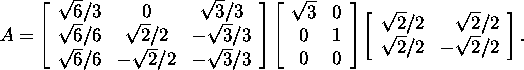
Kasutades definitsiooni 4.2.1 leiame pseudopöördmaatriksi
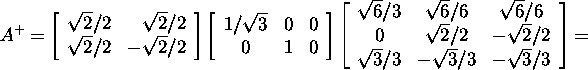
![]()
Süsteemi optimaalne lahend avaldub kujul
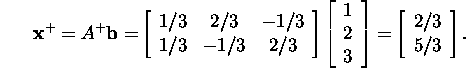
Ülesanne 4.2.2.* Leidke maatriksi A=[0] pseudopöördmaatriks ja selgitage saadud tulemust. Vastus: A+=[0].
Ülesanne 4.2.3.* Leidke maatriksi
A pseudopöördmaatriks, kui
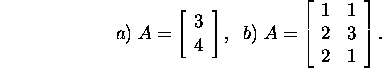
Ülesanne 4.2.4.* Milline on ortonormeeritud veergudega maatriksi A pseudopöördmaatriks? Vastus: A+=AT.
Ülesanne 4.2.5.* Leidke süsteemi
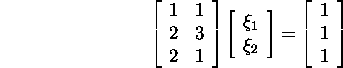
optimaalne lahend.
Lause 4.2.3 (Moore-Penrose'i tingimused).
Kui ![]() siis tingimusi
siis tingimusi
![]()
rahuldab vaid üks maatriks ![]() ja selleks on A+.
ja selleks on A+.
Ülesanne 4.2.6.* Maatriksit A
nimetatakse projektsioonimaatriksiks kui
![]()
Kontrollige projektsioonimaatriksi A korral Moore-Penrose'i
tingimuste täidetust. Kas A+=A?