Peatüki algus: Vektorid
Eelmine: Skalaarkorrutis
Järgmine: Ortogonaalsed vektorid

Definitsioon 1.5.1. Vektorruumi (üle arvukorpuse ) nimetatakse normeeritud ruumiks, kui igale vektorile on vastavusse seatud kindel, vektori normiks nimetatav, mittenegatiivne reaalarv nii, et on täidetud tingimused:

1. samasuse aksioom);

2. (homogeensuse aksioom);

3. (kolmnurga võrratus).

Definitsioon 1.5.2. Normeeritud ruumis kahe vektori vaheline kaugus defineeritakse valemiga

Lause 1.5.1 (Hölderi võrratus). Kui

siis

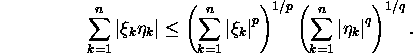
Tõestus. Vaadake E.Oja, P.Oja (1991, lk 11-12).

Lause 1.5.2 (Minkowski võrratus). Kui

siis

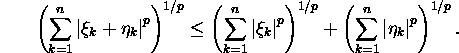
Tõestus. Vaadake E.Oja, P.Oja (1991, lk 10-11).

Näide 1.5.1. Vektorruumis tuuakse sisse vektori p-norm seostega



Veendume, et p-norm rahuldab definitsioonis 1.5.1 esitatud tingimusi 1-3 :

;

kasutades Minkowski võrratust, saame



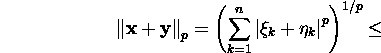
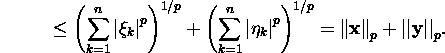
Veenduge tingimuste 1-3 täidetuses normi korral!
Enamkasutatavad p-normid on:

Ülesanne 1.5.1.^* Olgu antud vektorid ja Leidke

Lause 1.5.3. Ruumi kõik p-normid on ekvivalentsed, st kui ja on ruumi p-normid, siis leiduvad sellised positiivsed konstandid 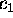ja et

Seejuures

Tõestame kolm viimast väidet:



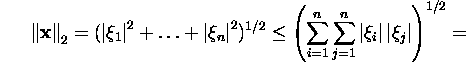
Hölderi võrratust kasutades, saame p=q=2 korral, et

Lause 1.5.4. Skalaarkorrutamisega ruum X on normeeritud ruum normiga

Tõestus. Kontrollime normi tingimuste 1-3 täidetust:












Siinjuures on kompleksarvu reaalosa tähistus.

Lause 1.5.5. Skalaarkorrutisega normeeritud ruumis kehtib rööpküliku reegel

Tõestus. Vahetu kontrolliga saame, et

Definitsioon 1.5.3. Öeldakse, et jada ruumi elementidest koondub p-normi suhtes elemendiks ja kirjutatakse , kui

Märkus 1.5.1. Kuna kõik ruumi p-normid on ekvivalentsed, siis jada koonduvusest -normi suhtes järeldub jada koonduvus -normi suhtes.

Ülesanne 1.5.1. Näidata, et kui , siis

Ülesanne 1.5.2. Näidata, et kui , siis

kusjuures ja ,. Leida selline konstant c_n, et

Definitsioon 1.5.4. Vektori lähendiks nimetatakse vektorit , mis teatavas mõttes erineb vähe vektorist

Definitsioon 1.5.5. Fikseeritud vektori normi korral nimetatakse vektori x lähendi absoluutseks veaks suurust

ja vektori lähendi relatiivseks veaks suurust

Relatiivset viga võib -normi korral käsitleda kui õigete tüvenumbrite näitajat. Nimelt, kui siis vektori suurimal komponendil on k õiget tüvenumbrit.

Näide 1.5.2. Olgu ja Leida ja ning lähendi suurima komponendi õigete tüvenumbrite arv abil. Leiame, et ja ning Seega suurimal komponendil on kolm õiget tüvenumbrit. Samal ajal on komponendil vaid üks õige tüvenumber.

Peatüki algus: Vektorid
Eelmine: Skalaarkorrutis
Järgmine: Ortogonaalsed vektorid