Peatüki algus: Pseudo-pöördmaatriks
Eelmine: Pseudo-pöördmaatriks
Järgmine: Pseudo-pöördmaatriks ja optimaalne lahend

Vaatleme lineaarse võrrandisüsteemi

 
lahendamist vähimruutude meetodil, juhul, kui ei ole täidetud Kronecker-Capelli teoreemi tingimus, st süsteem ei ole lahenduv tavalises mõttes.

Näide 4.1.1. Olgu süsteemiks

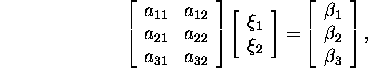
kus ja rank(A)=2. Olgu vektori ristprojektsioon ruumile Kuna vektor rank(A)=2, siis süsteem on üheselt lahenduv. Arvestades, et saame, et ja ehk
 
Süsteemi (2) maatriks A^TA on regulaarne, sest rank(A)=2. Järelikult on süsteem (2) esitatud tingimustel üheselt lahenduv ja
 
Hälbe normi ruudu

minimiseerimisel ( ) jõuame sama süsteemini (2) ja järelikult ka valemiga (3) määratava lahendini , võrrandi (1) lahendini vähimruutude mõttes.

Näites 4.1.1 esitatud mõttekäik on realiseeritav ka üldisemal juhul.

Definitsioon 4.1.1. Kui siis süsteemi (2) nimetatakse süsteemi (1) normaalvõrrandite süsteemiks.

Lause 4.1.1. Kui ja siis süsteemi (1) normaalvõrrandite süsteem (2) on üheselt lahenduv ja süsteemi (1) lahend vähimruutude mõttes avaldub kujul (3).

Näide 4.1.2.^* Lahendame vähimruutude mõttes võrrandisüsteemi

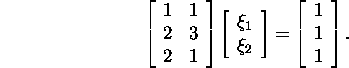
Moodustame normaalvõrrandite süsteemi

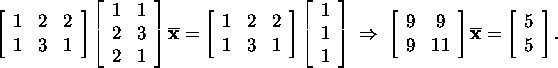
Seega

Kui ja ja rank(A)<n , siis normaalvõrrandite süsteemil (2) on lõpmata palju lahendeid, mis kõik avalduvad kujul

kusjuures ja Nende lahendite hulgast otsime vähima normiga, nn optimaalset lahendit Vektorite ja ortogonaalsusest järeldub, et

Kuna tingimusest järeldub, et siis

ja on võrrandi optimaalseks lahendiks . Seega,