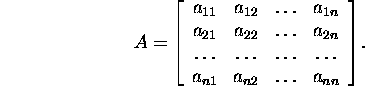
Peatüki algus: Maatriksid
Eelmine: Lintmaatriksid ja blokkmaatriksid
Järgmine: Maatriksi neli alamruumi

Vaatleme -maatriksit, nn n-järku maatriksit,

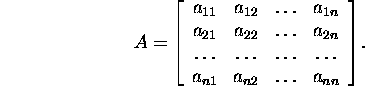
Definitsioon 2.3.1. Indeksite suvalist järjestust nimetatakse nende permutatsiooniks.

Definitsioon 2.3.2. Kahe indeksi järjekorda permutatsioonis nimetatakse loomulikuks kui väiksem indeks asetseb suuremast eespool; vastupidisel juhul - kui suurem indeks asetseb väiksemast eespool - öeldakse, et need kaks indeksit moodustavad inversiooni.

Definitsioon 2.3.3. Determinandiks nimetatakse eeskirja (kujutust, funktsiooni), mis seab ruutmaatriksile A vastavusse arvu, nn maatriksi determinandi,

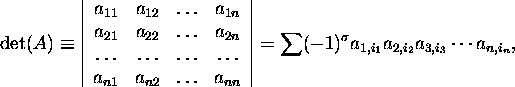
kus summeeritud on üle kõigi permutatsioonide indekseist ja on inversioonide arv veeruindeksite permutatsioonis . Räägitakse ka n-järku determinandist ja selle ridadest ning veergudest.

Näide 2.3.1. Vaatleme kolmandat järku determinanti





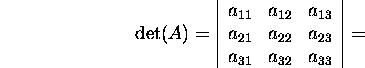
Selles esituses uurime näiteks viimast liidetavat (-1)³a₁₃a₂₂a₃₁. Selles veeruindeksite permutatsioonis 3 2 1 moodustab indeks 3 inversiooni indeksiga 2 ja indeksiga 1 ning indeks 2 moodustab inversiooni indeksiga 1. Seega inversioonide arv selles veeruindeksite permutatsioonis on võrdne kolmega.

Ülesanne 2.3.1.^* Millise märgiga kuulub determinandi avaldisse elementide korrutis

Determinantide omadused

• Transponeeritud maatriksi ja antud maatriksi determinandid on võrdsed,
• Determinandi mingi rea (veeru) kõigi elementide korrutamisel ühe ja sama arvuga korrutub determinant selle arvuga.
• Kui determinandis kahe rea (veeru) asukohad vahetada, siis muutub determinandi märk vastupidiseks.
• Kui determinandis kaks rida (veergu) on võrdsed, siis võrdub determinant nulliga.
• Kui determinandis mingi rea (veeru) iga element on kahe liidetava summa, siis see determinant lahutub kahe determinandi summaks, kusjuures esimeses determinandis on vaadeldavas reas (veerus) esimesed liidetavad ja teises determinandis selles reas (veerus) teised liidetavad ning ülejäänud read (veerud) on samad mis lähtedeterminandis:
  
  
• Determinant ei muutu, kui determinandi mingile reale (veerule) liita mistahes arvuga korrutatud teine rida (veerg).
• kehtivad on determinantide teooria põhivalemid (ehk arendusteoreemid):
  
  
  
  kus
  
  on Kroneckeri sümbol ja A_ik on maatriksist A i-nda rea ja k-nda veeru kustutamisel saadud -maatriksi determinandi ja arvu (-1)^i+k korrutis.

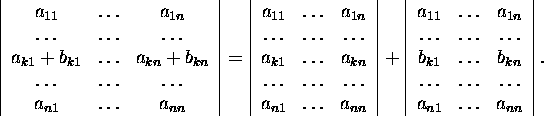
Näide 2.3.2. Arvutame n-järku determinandi, kasutades arendusteoreemi esimese veeru järgi ja siis esimese rea järgi, saame

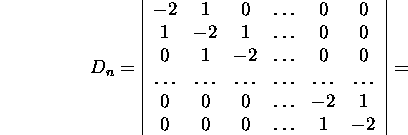
kus

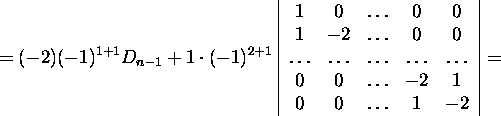
kus

ehk

Võrrand (1) on lineaarne homogeenne konstantsete kordajatega teist järku diferentsvõrrand, millel on lahendid tüüpi Üritame leida

Meid huvitavad mittetriviaalsed lahendid. Seega oleme saanud diferentsvõrrandi (1) lahendite määramiseks ruutvõrrandi

mille lahendeiks on ning võrrandi (1) üheks lahendiks on D_n=(-1)ⁿ. Kuna arv -1 on saadud ruutvõrrandi kahekordne lahend, siis võrrandi (1) lahendiks on ka D_n=(-1)ⁿn. Seega oleme kätte saanud lineaarse homogeense konstantsete kordajatega teist järku diferentsvõrrandi (1) kaks lineaarselt sõltumatut erilahendit ja selle võrrandi üldlahend avaldub kujul

Tingimustest D₁=-2 ja D₂=3 saame määrata kordajad C₁ ja C₂:

st saame meie konkreetse ülesande vastuse

Ülesanne 2.3.3.^* Arvutage Laplace'i valemi abil determinant

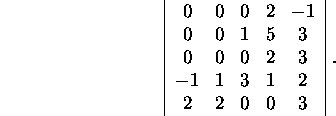
Näide 2.3.3. Leiame Vandermonde'i determinandi

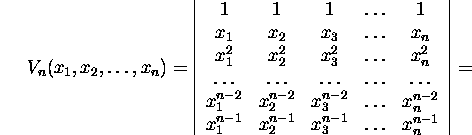
lahutades determinandi viimasest reast arvuga x₁ korrutatud eelviimase rea, siis eelviimasest reast arvuga x₁ korrutatud (n-2)-se rea, siis (n-2)-st reast arvuga x₁ korrutatud (n-3)-nda rea jne., viimasena teisest reast arvuga x₁ korrutatud esimese rea. Tulemuseks saame

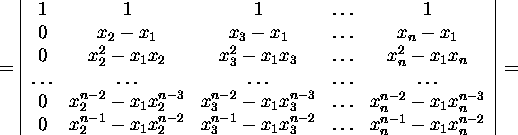
ja kasutades arendust esimese veeru järgi ning tuues elementides ühised tegurid sulgude ette, saame

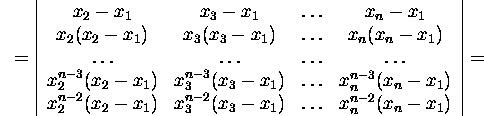
ning tuues esimesest veerust ette ühise teguri x₂-x₁ ja teisest veerust , (n-1)-st veerust x_n-x₁, sa ame

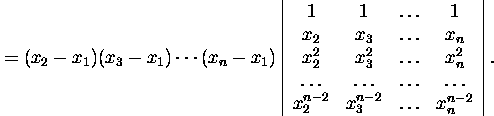
Kasutades samu operatsioonide tsükleid jõuame tulemuseni

Lause 2.3.1 (Laplace'i arendusteoreem). Kehtib nn Laplace'i valem

kusjuures paremal seisev summa tuleb võtta üle kõigi k-järku determinantide (miinorite) M_k, mida saab moodustada ridadest i₁, i₂, , i_k ja A_n-k on maatriksist A miinori M_k moodustamisel kasutatud ridade i₁, i₂, , i_k ning veergude j₁, j₂, , j_k kustutamisel saadud maatriksi determinandi korrutis arvuga

Tõestus. Vaadake Kangro (1962, lk 37-39).

Näide 2.3.4. Kasutades Laplace'i arendust kahe esimese rea järgi teisendada determinanti

Kuna maatriksi kahe esimese rea elementidest saab moodustada vaid kolm nullist erinevat miinorit , siis saame arenduse

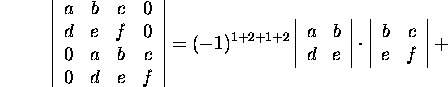
Ülesanne 2.3.3.^* Arvutage Laplace'i valemi abil determinant

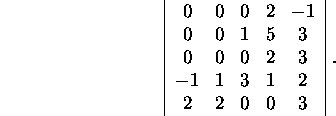
Laplace'i arendusteoreemi põhjal peab paika seos
 
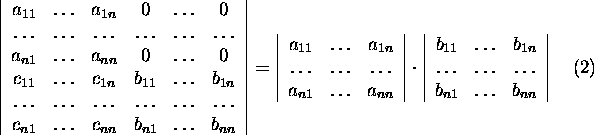
suvalise maatriksi

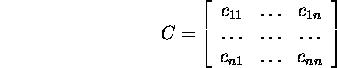
korral. Valides

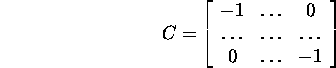
teisendame determinanti

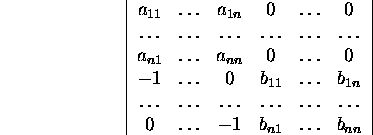
nii, et kõik b_ij saaksid nullideks. Et muuta nullideks tuleb (n+1)-sele veerule liita elemendiga b₁₁ korrutatud esimene veerg ja elemendiga b₂₁ korrutatud teine veerg jne ning lõpuks elemendiga b_n1 korrutatud n-is veerg. Järgmisena muudame nullideks Selleks liidame (n+2)-sele veerule elemendiga b₁₂ korrutatud esimese veeru ja elemendiga b₂₂ korrutatud teise veeru jne ning lõpuks elemendiga b_n2 korrutatud n-nda veeru jne. Viimase sammuna muudame nullideks Selleks liidame 2n-dale veerule elemendiga b_1n korrutatud esimese ve eru ja elemendiga b_2n korrutatud teise veeru jne ning lõpuks elemendiga b_nn korrutatud n-nda veeru. Tulemuseks saame





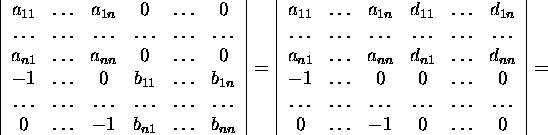
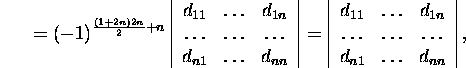
kus
 
Arvestades seost (2) ja seda, et seose (3) põhjal D=A^.B, jõuame väiteni

Lause 2.3.1 (teoreem maatriksite korrutise determinandist). Mistahes kahe n-järku maatriksi A ja B korral

Peatüki algus: Maatriksid
Eelmine: Lintmaatriksid ja blokkmaatriksid
Järgmine: Maatriksi neli alamruumi