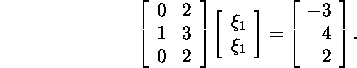Let us consider the system
where A=QR is a QR
factorization of the regular matrix 
,
while 
is an orthogonal matrix and 
ia on upper triangular matrix. Substituting in (14) the matrix A
by its QR factorization,
we get
Multiplying the both sides of equality (15) on the left
by the matrix QT, we find
System (16) has an upper triangular matrix R.
From the regularity of the matrix A it follows the regularity of the matrix
R. Hence system (16) is uniquely solvable. For
this the substitution given in proposition
1.1.2 will be used backwards.
Example 6.7.1. Let us solve the system
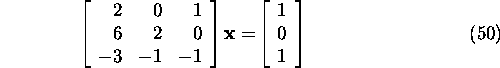
using the QR method.
In example 2.3.2 the
QR factorization
of the matrix of the system
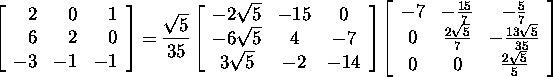
was found. We respect system (17) in form (16):
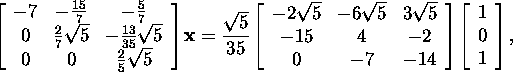
i.e.,
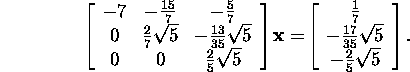
We solve the obtained system with the upper triangular matrix using the
backwards substitution. The result
is 
Let us consider the solving of system (14),
where A=QR is a QR
factorization of the regular matrix 
,
where 
is an orthogonal matrix and
is an upper triangular matrix, by the least-squares
method. Let
and
where 
and 
We find
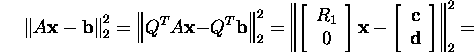
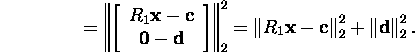
Since the quantity 
is a constant, we can minimize only the quantity
and the minimal value of it is 0. Really, from the condition 
it follows that the matrix R1 is regular. Hence the system
where by the symbol 
it is denoted the least-squares
solution of system (14), is uniquely solvable.
Example 6.7.2. Let us find the
least squares solution of the system
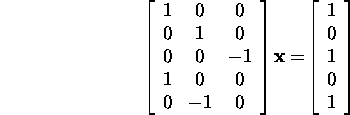
using the QR method.
Using the software package ``Maple'', we obtain the
QR factorization of the matrix of the system
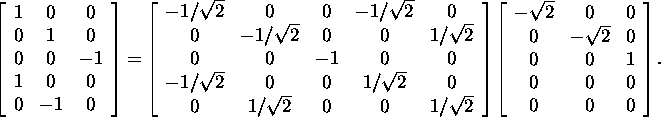
From this factorization it appears that
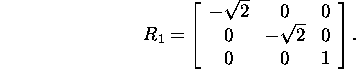
To get the vector 
,
we find
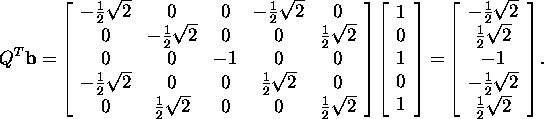
Hence
We det for the concrete form of the system 
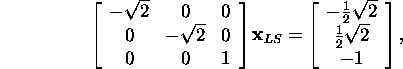
from which it follows that
Example 6.7.3.* Let us find the least-squares
solution of the system
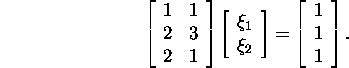
In example 2.3.3 it was found the QR
factorization of the matrix of the system:
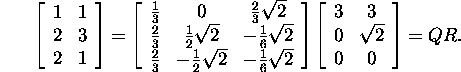
Omitting the last row of zeros in the matrix R, we get
Now we find
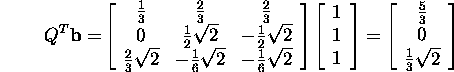
Taking the first two components of this vector (the matrix R1
has two rows), we obtain
We get the least-squares solution
of the initial system from 
i.e.,
Problem 6.7.1.* Solve the system of
equations
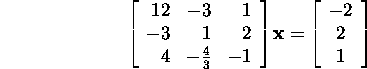
knowing the QR
factorization of the system matrix
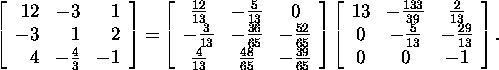
Problem 6.7.2.* Find the least-squares
solution of the system
