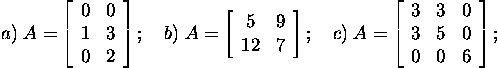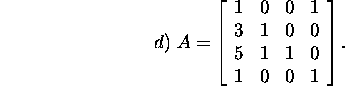Householder QR Factorization

Apply the Householder reflection to the matrix to obtain the QR factorization.

Example 2.3.1. Suppose and assume that the Householder matrices H₁ and H₂ have been computed so that

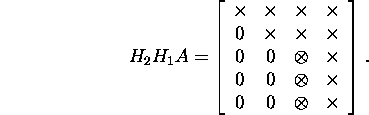
Concentrating on the highlighted vector , we determine a Householder matrix such that

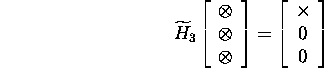
Choosing we get

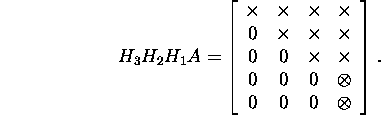
Next consider the highlighted vector and determine such that

Choosing we have

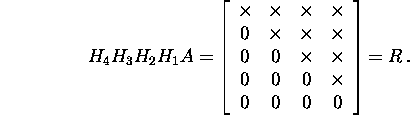
By setting Q=H₁H₂H₃H₄, we obtain QR=H₁H₂H₃H₄H₄H₃H₂H₁A=A.

Proposition 2.3.1. If then there exist the Householder matrices such that



and

where is orthogonal and is upper triangular.

Example 2.3.2. Find the Householder QR factorization for

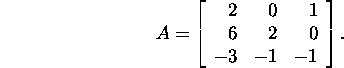
In example 2.1.1 there has been found the Householder matrix for the transformation of the first column vector of A:

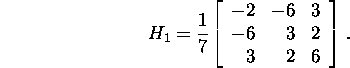
Find that

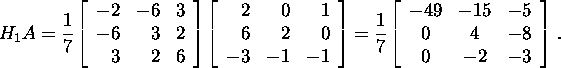
To find we compute the according Householder vector

Hence

and

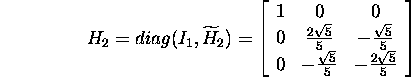
and also



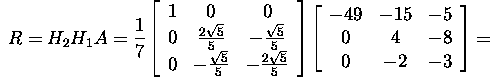
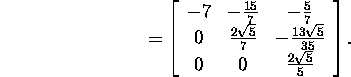
Find also the orthogonal matrix



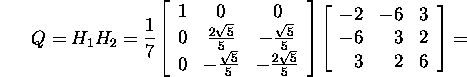
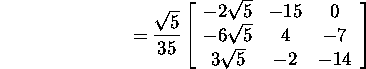
and check the result

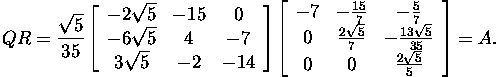
Example 2.3.3^*. Find the Householder QR factorization of


The vector that has to be transformed is where Construct the vector

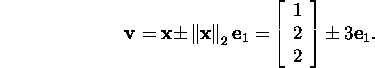
Choose the sign minus for the coefficient of and take into account that H depends only on the direction of :

Find the Householder matrix



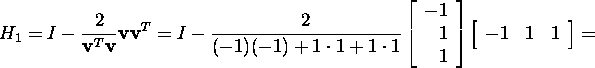
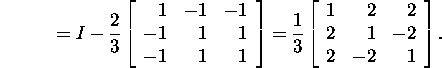
Verify that H₁ annihilates all the elements of the first column of A but the first one. Indeed,

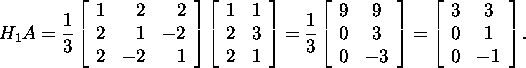
Further we transform the vector where Find the Householder vector according to

Choose the sign minus for coefficient of :

We obtain the Householder matrix according to this vector





and find that

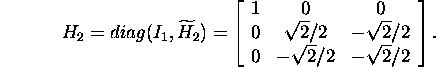
Thus,

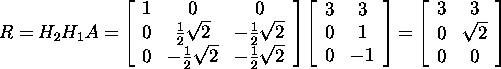
and

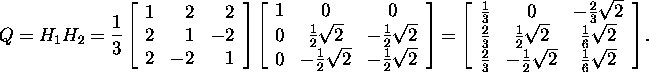
Let us check the result:

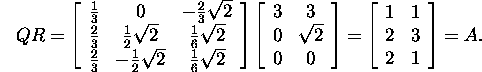
Exercise 2.3.1.^* Find the QR factorization of A if