Let us consider the solution
of a system of linear equations
by the least-squares method in the case the condition of the Kronecker-Capelli
theorem is not satisfied, i.e., the system has no solution in ordinary
sense.
Example 4.1.1. Let
the system be
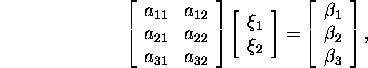
where 
and rank(A)=2. Let 
be the orthogonal projection
of the vector 
onto the space 
Since the vector 
and rank(A)=2, the system 
has a unique solution. Taking into consideration that 
we get 
and 
or
The matrix ATA of the system (2) is
regular since rank(A)=2. Therefore the system (2)
is uniquely solvable on the given conditions and
By minimizing the square of the norm of discrepancy 
( 
),
we obtain the same system (2), and hence the same solution
determined by the formula (3), the least-square
solution of the equation (1).
The line of reasoning given in example 4.1.1 can be realized also in a more general case.
Definition 4.1.1.
If 
then system (2) is called the system of normal equations of system
(1).
Proposition 4.1.1.
If
and suppose rank(A)=n, then the system
of normal equations (2) of system (1) is uniquely
solvable and the least-squares solution
of the system (1) is given by (3).
Example 4.1.2.* Let us solve by the
least-squares method the system of
equations
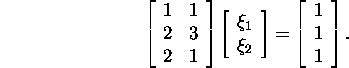
We form the system of normal
equations 
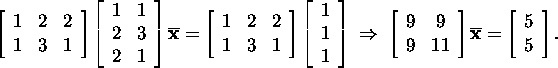
Thus,
If 
,
and rank(A)<n, then the system of normal equations
(2) has infinite number of solutions, which can be all
expressed as
where 
and 
From among the solutions
we will find the one having the least norm, the so-called optimum
solution 
From the orthogonality of the
vectors 
and 
it follows that
Since from
it follows 
then
and
is the optimum solution 
of the equation 
.
Thus, 
