Let us consider the solution of a 
lower triangular system
by forward substitution. From the first equation we obtain 
and then from the second 
Proposition 1.1.1
( forward substitution). If 
is a lower triangular matrix, 
and 
then the solution is
Solve the upper
triangular system
by back substitution. From the second equation we obtain 
and then from the first one 
Proposition 1.1.2 (back
substitution). If 
is an upper triangular matrix, 
and 
then the solution is
In case of forward substitution
as well as in case of back substitution the
solution of the system with a regular 
triangular
matrix requires 
operations.
Proposition 1.1.3 (forward
substitution: row version). If 
is lower triangular, 
,
and 
has been found, then after substitution of 
into
the equations from the second to the n-th, we obtain a new 
lower triangular system
Proposition 1.1.4 (back
substitution:column version). If 
is upper triangular, 
,
and 
has been found, then after the substitution of
into the equations from the first to the (n-1)-th, we obtain a new
upper
triangular system
Now we consider the simultaneous solution of several systems
with a common system matrix. Let us consider the system LX=B,
where
is a regular lower triangular matrix, 
and the wanted is 
.
We represent this system in block form
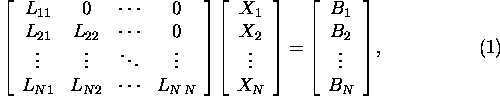
where the diagonal blocks are square. From the equation 
we can find X1. By using for system (1)
the row version given in Proposition 1.1.3,
we obtain
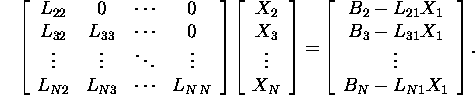
Continuing in this way we obtain the solution of system (1).
Proposition 1.1.5. Triangular matrices have the following properties: