Matrix Diagonalization

In proposition 1.2.6.8 on the Jordan decomposition it is stated that if then there exists such a regular that
 
where and

is a Jordan block or Jordan box, and the matrix J is called a Jordan canonical form or Jordan normal form of the matrix A. The number of Jordan blocks in decomposition (1) equals the number of the linearly independent eigenvectors of the matrix A. Namely, to each linearly independent eigenvector it corresponds one block. Hence if the matrix A has a basis of eigenvectors, then all the Jordan blocks are blocks, and the Jordan normal form coincides with the diagonal form of the matrix given in proposition 1.2.5.8 where and the matrix S has for columns the linearly independent eigenvectors of the matrix A corresponding to these eigenvalues.

Example 5.1.1.^* Let us find the Jordan form of the matrix

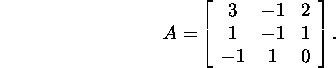
We shall find the eigenvalues of the matrix A:

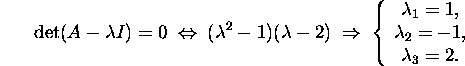
Now we shall find the eigenvectors corresponding to these eigenvalues:





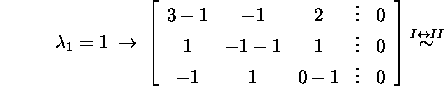
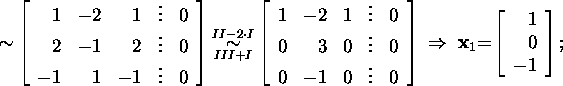
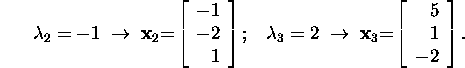
We compile the matrix of eigenvectors of the matrix A

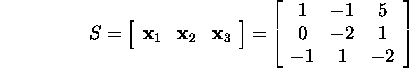
and find the inverse matrix

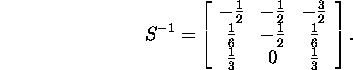
As the result, we obtain

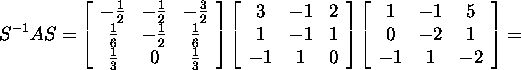
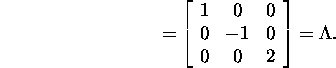
Proposition 5.1.1. Any Hermitian (symmetric) matrix can be taken to the diagonal form using a unitary matrix (an orthogonal matrix i.e., there exists such that
 

Proof. The Schur factorisation (proposition 1.2.6.5) implies that the Hermitian matrix can be given in the form
 
where is a unitary matrix and is an upper triangular matrix. Finding the transpose conjugate matrices of both sides of (3), we get

In virtue of the Hermitian matrix definition A^H=A, we find that
 
From (3) and (4) it follows that T=D. The diagonal elements of the diagonal matrix D similar to the matrix A are the eigenvalues of the matrix A. The assertion about the symmetric matrix is a special case of the considered complex version.

Problem 5.1.1.^* Let

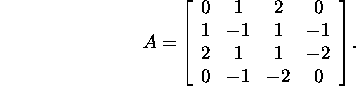
Find such an orthogonal matrix that where is a diagonal matrix.

Problem 5.1.2.^* Let

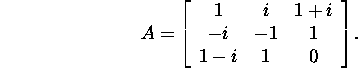
Find such a unitary matrix that where is a diagonal matrix.

Not every square matrix can be taken to form (2). Proposition 1.2.6.6 implies that only a normal matrix can be expressed in form (2). In general case of the diagonalization of a matrix one must confine himself to the Jordan normal form (1).