Pseudoinverse Matrix and Optimum Solution

Next we will consider the algorithm of finding the optimum solution.

Example 4.2.1. Let and

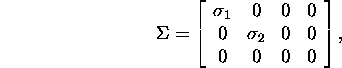
where and We will find the optimum solution of the system

The orthogonal projection of the vector on the space is , and To find the solution , one must solve the system

i.e.,

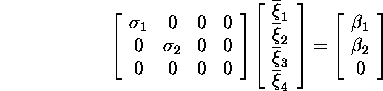
or

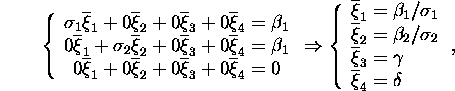
where are arbitrary. Taking we obtain the solution with the least 2-norm

We state that can be expressed also by

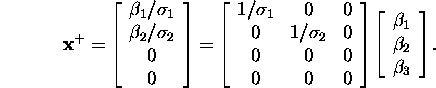
The optimum solution of the given example can be obtained from the vector by multiplying it on the left by the matrix

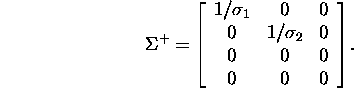
The matrix is got from the matrix by its transposing and afterwards replacing the nonzero entries by their reciprocals. Hence

Let us generalize the result obtained in example 4.2.1.

Proposition 4.2.1. If
 
and
 
then the optimum solution of the system

is given by

where
 

Definition 4.2.1. Let

be the singular value decomposition of the matrix . The pseudoinverse matrix of the matrix A is a matrix

where and are given by relations (1-3).

Problem 4.2.1. Let and Show that A⁺=A^-1.

Problem 4.2.2. Let us find the pseudoinverse matrix of the matrix given in example 3.3.2. We found the singular value decomposition of the matrix A in this example

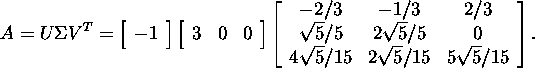
On the ground of definition 4.2.1,

i.e.,

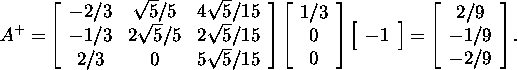
Proposition 4.2.2. If then the optimum solution of the system (in the sense of least-squares) is given by

Proof. When a vector is multiplied by the orthogonal matrix U^T, its 2-norm conserves. Therefore,

Let substitute Hence

Proposition 4.2.1 implies that the minimizing vector for the expression is the vector

and the vector

minimizes the expression

Example 4.2.3. Let us find the optimum solution of the system

In example 4.2.2, we found the pseudoinverse matrix

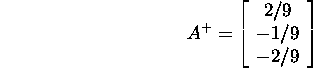
of the matrix of the system

In virtue of proposition 4.2.2, we get the optimum solution

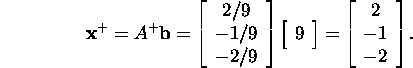
Example 4.2.4. Let us find the optimum solution of the system

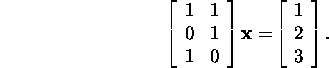
In example 3.3.1, we found the singular value decomposition of the system matrix A

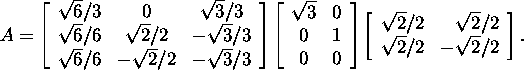
Using definition 4.2.1, we will find the pseudoinverse matrix



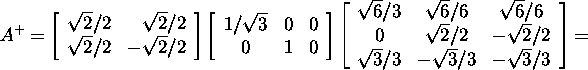
The optimum solution of the system will be

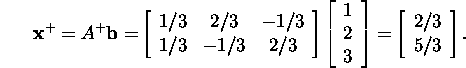
Problem 4.2.2.^* Find the pseudoinverse of the matrix A=[0] and explain the result. Answer: A⁺=[0].

Problem 4.2.3.^* Find the pseudoinverse of the matrix A

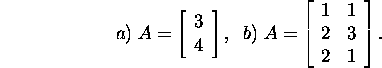
Problem 4.2.4.^* What is the pseudoinverse matrix of the matrix A with orthogonal columns? Answer: A⁺=A^T.

Problem 4.2.5.^* Find the optimum solution of the system

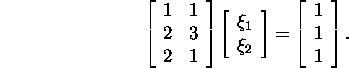
Proposition 4.2.3 (Conditions of Moore-Penrose.) If then the conditions

are satisfied only by one matrix , and this is A⁺.

Problem 4.2.6.^* A matrix A is called projectionmatrix if

Check the Moore-Penrose conditions for the projectionmatrix. Does A⁺=A?