Peatüki algus: LU-lahutus
Eelmine: Kolmnurksete võrrandisüsteemide lahendamine
Järgmine: QR-lahutus

Teatud tingimustel on võrrandisüsteemi süsteemimaatriks A esitatav alumise ühikdiagonaaliga, st peadiagonaali elementideks on ühed, kolmnurkmaatriksi L ja ülemise kolmnurkmaatriksi U korrutisena ja lahendada tuleb kaks kolmnurkse maatriksiga võrrandisüsteemi.

Lause 1.2.1 (LU-meetod). Kui kus L on alumine ühikdiagonaaliga kolmnurkmaatriks ja U on ülemine regulaarne kolmnurkmaatriks, ning siis ning süsteemi lahendamiseks tuleb alguses lahendada süsteem ja seejärel lahendada süsteem

Näide 1.2.1. Lahendame süsteemi

LU-meetodil. Kuna

siis lause 1.2.1 põhjal tuleb, esiteks, lahendada süsteem

Selle süsteemi lahendiks on ja Teiseks, lahendades süsteemi

leiame, et ja Seega,

Lineaaralgebra põhikursuses võrrandisüsteemide lahendamiseks esitatud Gaussi võte on rakendatav ka LU-lahutuse korral. Olgu kusjuures Kui

ja
 
siis

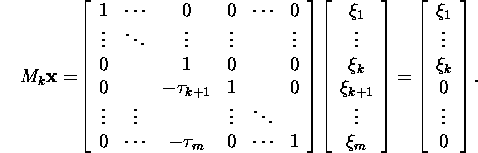
Definitsioon 1.2.1. Maatriksit M_k kujul (2) nimetatakse Gaussi maatriksiks, komponente nimetatakse Gaussi kordajateks ja vektorit Gaussi vektoriks ning Gaussi maatriksiga määratud teisendust nimetatakse Gaussi teisenduseks.

Definitsioon 1.2.2. Maatriksi k-ndaks juhtelemendiks nimetatakse suurust

kusjuures ja

Kui siis maatriksi A nullist erinevate juhtelementide korral on leitavad Gaussi maatriksid nii, et on ülemine kolmnurkmaatriks.

Näide 1.2.2. Vaatleme Gaussi maatriksite M₁ ja ning ülemise kolmnurkmaatriksi U leidmist maatriksi

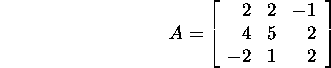
korral. Seose (2) abil leiame, et



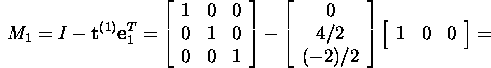
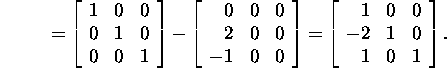
Seega,

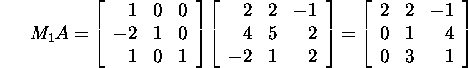
ja



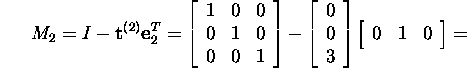
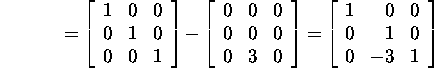
ning

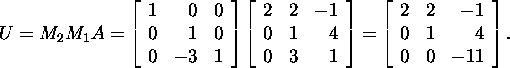
Märgime, et maatriks on ülemine kolmnurkne veergudes ühest kuni (k-1)-ni ja Gaussi maatriksi M_k elementide arvutamiseks kasutatakse maatriksi vektorit A^(k-1)(k:m,k), kusjuures maatriksi M_k leidmine on võimalik, kui . Lisaks, Kui valida

siis

Rõhutame, et meie käsitluses alumine kolmnurkmaatriks L on ühikdiagonaaliga maatriks.

Lause 1.2.2. Kui peamiinorid, so 1: k , 1: 1: n-1), siis maatriksil on olemas LU-lahutus. Kui regulaarsel maatriksil A eksisteerib LU-lahutus, siis see on ühene ja

Tõestus. Oletame, et k-1 sammu on sooritatud ja leitud on maatriks Element a_kk^(k-1) on maatriksi A k-s juhtelement ja 1:k, 1: Seega, kui A(1:k, 1:k) on regulaarne, siis ja eksisteerib maatriksi A jaoks LU-lahutus. Oletades, et regulaarsel maatriksil A on kaks LU-lahutust A=L₁U₁ ja A=L₂U₂, saame, et L₁U₁=L₂U₂ ehk L₂^-1L₁=U₂U₁^-1. Kuna L₂^-1L₁ o n alumine kolmnurkmaatriks, mille peadiagonaalil on ühed ja U₂U₁^-1on ülemine kolmnukmaatriks, siis L₂^-1L₁=I ja U₂U₁^-1=I ning L₂=L₁ ja

Näide 1.2.3.^* Leiame maatriksi

LU-lahutuse.
Leiame Gaussi maatriksi M₁ maatriksi A korral:



Seega

ja

Näide 1.2.4.^* Leiame maatriksi

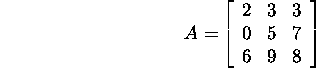
LU-lahutuse.
Leiame Gaussi maatriksi M₁ maatriksi A korral:



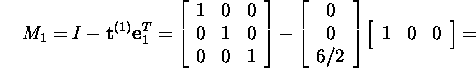
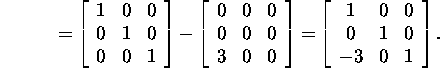
Seega

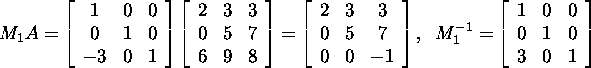
ja kuna maatriks M₁A on ülemine kolmnurkmaatriks, siis M₂=I ning

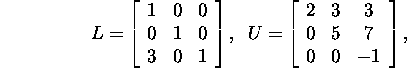
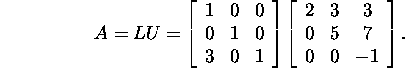
Näide 1.2.5.^* Lahendame süsteemi , kus

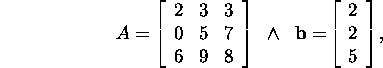
kasutades LU-lahutust.
Näites 1.2.4 on leitud maatriksi A jaoks LU -lahutus:

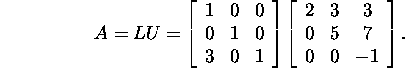
Süsteemi so

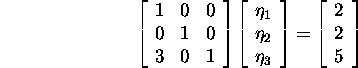
lahendamisel saame, et

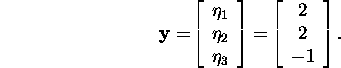
Süsteemi so

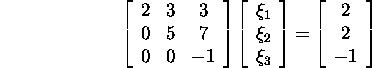
lahendamisel leiame, et

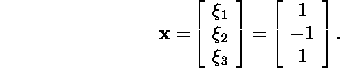
Ülesanne 1.2.1.^* Leidke maatriksi A jaoks LU-lahutus, kui

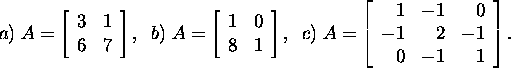
Ülesanne 1.2.2.^* Lahendage süsteem , kus

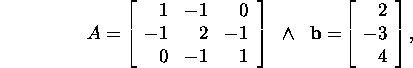
kasutades LU-lahutust.

Ka ristkülikmaatriksi , mille peamiinorid on nullist erinevad, so

jaoks eksisteerib LU-lahutus.

Näide 1.2.6. Järgnevad seosed peavad paika



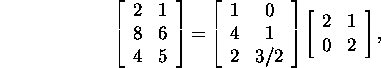
Algebra põhikursusest on teada, et Gaussi elimineerimismeetodi vahetu rakendamine , seega ka LU-lahutuse vahetu teostamine, nurjub, kui vähemalt üks maatriksi peamiinoreist on singulaarne. Osutub, et regulaarse maatriksi korral on peale maatriksi ridade järjekorra sobivat muutmist võimalik teisendatud maatriksi LU-lahutus. Ridade (ka veergude) järjekorra muutmiseks kasutatakse permutatsioonimaatrikseid.

Definitsioon 1.2.3. Permutatsioonimaatriksiks nimetatakse maatriksit, mis on saadud ühikmaatriksist I ridade järjekorra muutmise teel.

Näide 1.2.7 . Vaatleme, kuidas mõjub maatriksile A selle korrutamine ühe konkreetse permutatsioonimaatriksiga P.

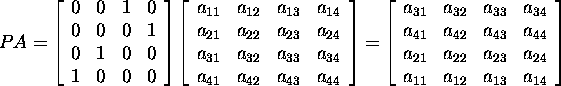
Permutatsioonimaatriksiga P vasakult korrutamisel saame uue maatriksi, mis on lähtemaatriksist saadud ridade samal viisil ümberpaigutamisel, kui on saadud maatriks P maatriksist I. Korrutades paremalt,

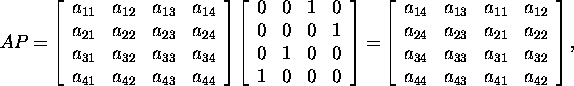
saame uue maatriksi, mis on lähtemaatriksist saadud veergudede samal viisil ümberpaigutamisel, kui on saadud maatriks P maatriksist I veergude ümberpaigutamise teel. Peab paika

Lause 1.2.3. Kui ja siis leidub selline permutatsioonimaatriks et maatriksi PA kõik peamiinorid on nullist erinevad ja seega eksisteerib LU-lahutus

Näide 1.2.8.^* Olgu

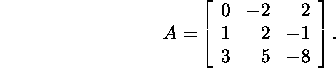
Leiame sobiva permutatsioonimaatriksi korral maatriksi PA jaoks LU-lahutuse.
Vahetame ära maatriksi A esimese ja teise rea, st võtame

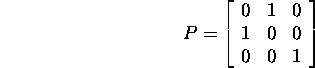
ning leiame maatriksi

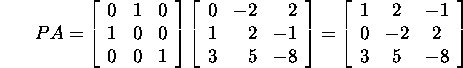
korral Gaussi maatriksi

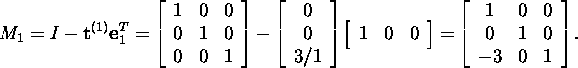
Seega

ja

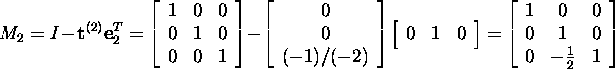
ning

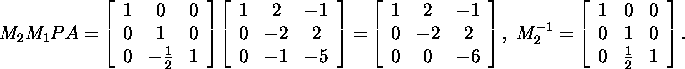
Järelikult,

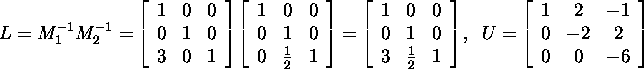
ja

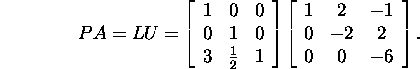
Ülesanne 1.2.3.^* Leiame sobiva permutatsioonimaatriksi P korral maatriksi PA jaoks LU-lahutuse, kui

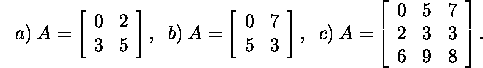
Peatüki algus: LU-lahutus
Eelmine: Kolmnurksete võrrandisüsteemide lahendamine
Järgmine: QR-lahutus